최소신장트리(MST)에 대한 이해
- 신장트리란, 뱡향성이 없는 그래프의 부분그래프(Subgraph)들 중에서, 모든 정점을 포함하는 트리이다.
- 최소신장트리란, 신장트리들 중에서 간선의 합이 가장 작은 트리를 말한다.
- 그래프에서 최소신장트리는 여러 개 있을 수 있다.
최소신장트리를 구하는 알고리즘으로는 크게 크루스칼(Kruscal) 알고리즘과 프림(Prim) 알고리즘이 있으며, 해당 글에서는 크루스칼 알고리즘의 방법을 다룬다.
V(노드의 개수) = 6, E(간선의 개수) = 7 인 다음과 같은 그래프에서 최소신장트리의 간선 길이의 합을 구해보자.
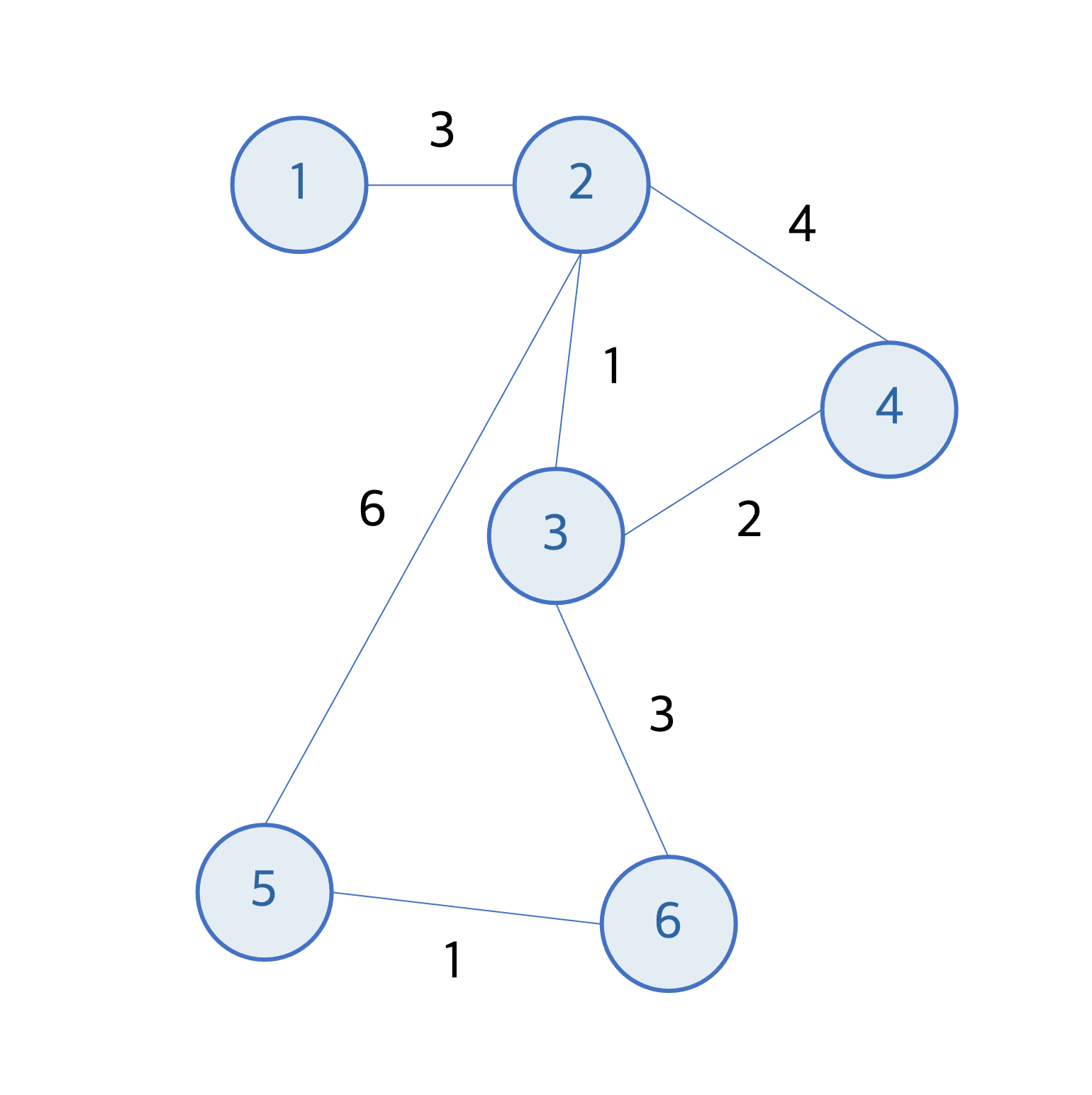
간선들 중, 가장 길이가 짧은 간선을 선택하여 연결된 두 노드를 확인한다. 만약 두 노드가 다른 집합에 속해있다면 두 노드를 같은 집합에 포함시키고 해당 간선을 최소신장트리에 포함시킨다. 현재 가장 짧은 간선은 길이가 1이면서 정점 2와 정점 3을 잇는 간선이다. 정점 2와 정점 3은 다른 집합에 속해있으므로 해당 간선을 선택하고 두 노드를 같은 집합으로 연결한다.

다음으로 짧은 간선을 선택하여 연결된 두 노드를 확인한다. 다음으로 짧은 간선은 길이가 1이면서 정점 5와 정점 6을 연결하는 간선이다. 정점 5와 정점 6은 다른 집합에 속해있으므로 해당 간선을 선택하고 두 노드를 같은 집합으로 연결한다.

다음으로 짧은 간선은 길이가 2이면서 정점 3과 정점 4를 연결하는 간선이다. 정점 3은 초록색 집합에 속해있고, 정점 4는 정점 4만을 원소로 갖는 집합에 속해있다. 정점 3과 정점 4는 다른 집합에 속해있으므로 해당 간선을 선택하고 두 노드를 같은 집합으로 연결한다.

다음으로 짧은 간선은 길이가 3이면서 정점 1과 정점 2를 연결하는 간선이다. 정점 1은 정점 1만을 원소로 갖는 집합에 속해있고, 정점 2는 초록색 집합에 속해있다. 두 정점은 다른 집합에 속해있으므로 해당 간선을 선택하고 두 노드를 같은 집합으로 연결한다.
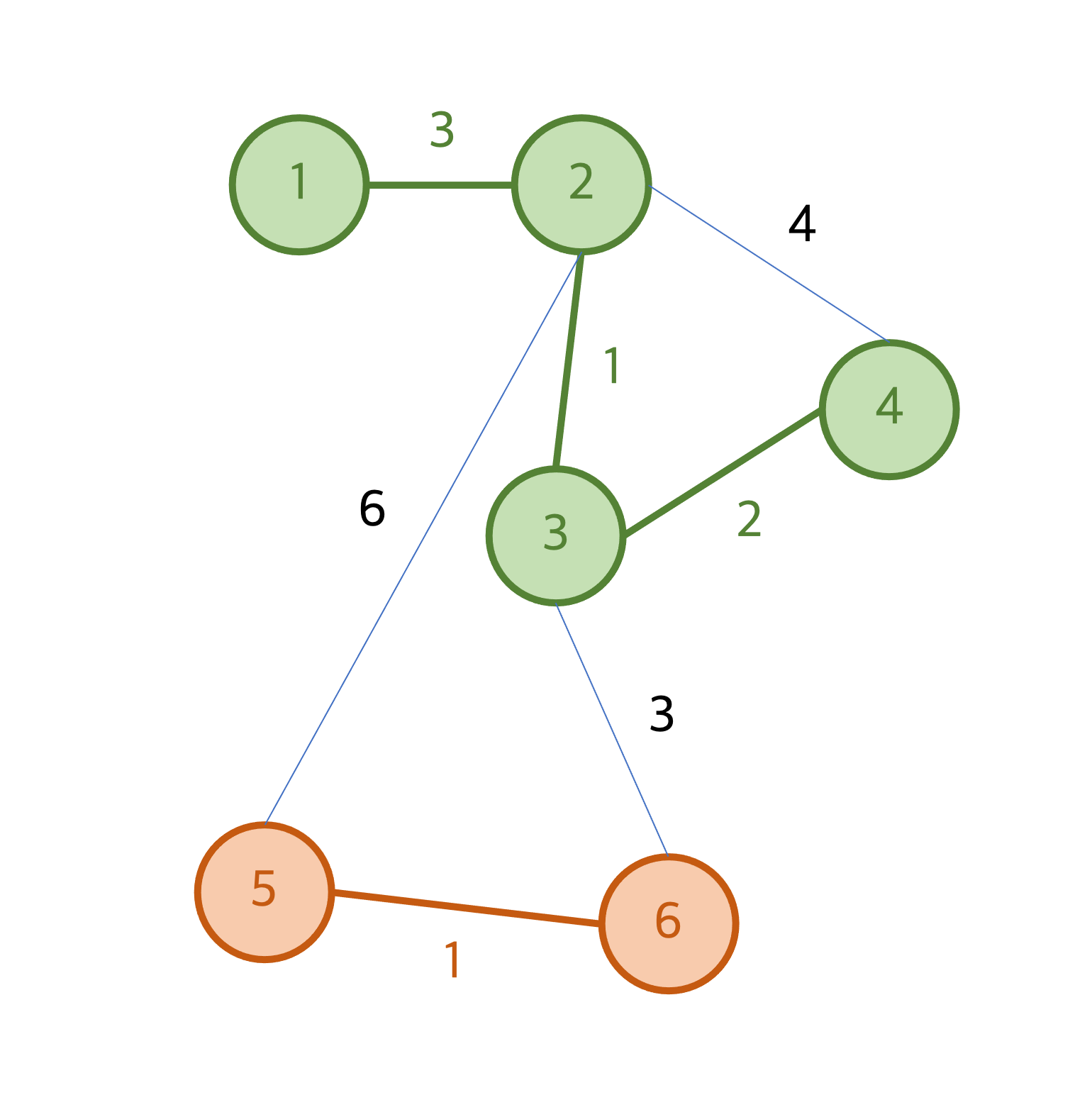
다음으로 짧은 간선은 길이가 3이면서 정점 3과 정점 6을 연결하는 간선이다. 정점 3은 초록색 집합에, 정점 6은 주황색 집합에 속해있으므로 해당 간선을 선택하고 두 노드를 같은 집합으로 연결한다.
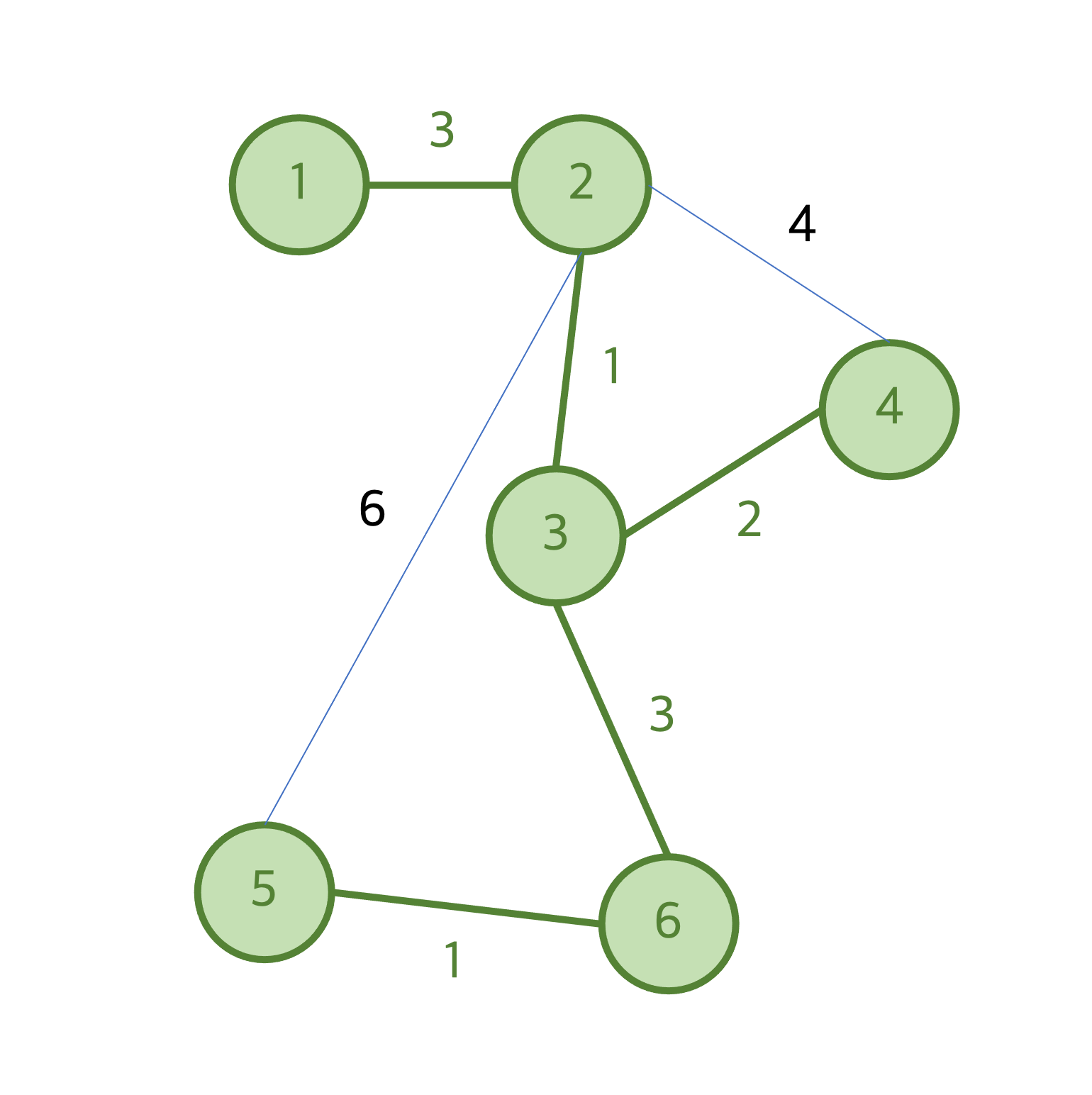
다음으로 짧은 간선은 길이가 4이고 정점 2와 정점 4를 연결하는 간선이다. 이 때, 정점 2번과 정점 4번은 이미 같은 집합에 속해있으므로 해당 간선을 선택하지 않고 넘어간다. 길이가 6인 마지막으로 짧은 간선 역시 정점 2와 정점 5가 이미 같은 집합에 속해있으므로 선택하지 않고 넘어간다.
지금까지 선택한 모든 간선의 길이의 합을 구해보면, 3+1+2+3+1 = 10 이다.
전체 코드
참고) 최소신장트리를 구현하기 위해서는 Union-Find 알고리즘이 필요하다.
#include <vector>
#include <tuple>
#include <algorithm>
#include <iostream>
using namespace std;
using iii = tuple<int, int, int>;
int N, M; //노드 개수, 간선의 개수
int tot;
vector<iii> edge;
vector<int> parent(1005, 0), nrank(1005, 1);
void setEdge() {
for (int i=0; i<M; i++) {
int u, v, w; //정점 u와 v를 연결할 때 길이(비용) w
scanf("%d %d %d", &u, &v, &w);
edge.push_back({w, u, v});
}
sort(edge.begin(), edge.end()); //길이가 짧은 간선부터 선택하기 위해 정렬
}
void initialize() {
for (int i=1; i<=N; i++) parent[i] = i;
}
int find(int u) {
if (parent[u] == u) return u;
return parent[u] = find(parent[u]);
}
void merge(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
if (nrank[u] > nrank[v]) swap(u, v);
if (nrank[u] == nrank[v]) nrank[v]++;
parent[u] = v;
}
void kruscal() {
for (auto x : edge) { //길이(비용)이 짧은 간선 부터 선택
int cost, u, v;
tie(cost, u, v) = x;
if (find(u) == find(v)) continue; //간선의 두 정점이 이미 같은 집합이라면 넘어감
merge(u, v); //다른 집합이라면 두 정점을 합친 후 간선 선택
tot += cost;
}
}
int main() {
scanf("%d %d", &N, &M);
setEdge();
initialize();
kruscal();
printf("%d", tot);
return 0;
}
/*
input:
6 7
1 2 3
2 3 1
2 5 6
2 4 4
3 4 2
3 6 3
5 6 1
output:
10
*/
크루스칼 알고리즘의 시간복잡도
간선의 양 끝 정점이 같은 집합에 속해있는지 확인하는 Union-find 알고리즘은 상수의 시간복잡도를 가진다. 따라서 크루스칼 알고리즘의 시간복잡도는 간선들을 정렬하는 연산과 비례하고, 시간복잡도는 O(ElogE)이다.
'Computer Basics > Algorithm Techniques' 카테고리의 다른 글
| 완전탐색_순열/중복순열/조합/중복조합 (0) | 2022.03.11 |
|---|---|
| 최단거리구하기_플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2022.03.07 |
| 유니온파인드(Union-Find) (0) | 2022.03.03 |
| 위상정렬(Topological sort) (0) | 2022.03.01 |
| 트리_그래프가 트리인지 확인하는 방법 (0) | 2022.02.28 |
댓글