위상정렬
- 위상정렬이란, 사이클이 없는 방향 그래프(DAG: Directed Acyclic Graph)에서 정점 사이의 선후 관계를 위배하지 않고 정렬하는 알고리즘이다.
- 흔히 선수과목들의 수강 순서를 정하는 문제가 위상정렬에 비유된다.
- 정해진 순서를 위배하지 않고 정렬하는 방법은 여러가지가 있을 수 있다.
위상정렬의 과정
N(노드의 개수) = 7, M(간선의 개수) = 7 인 다음과 같은 그래프에서 위상정렬을 수행해보자.
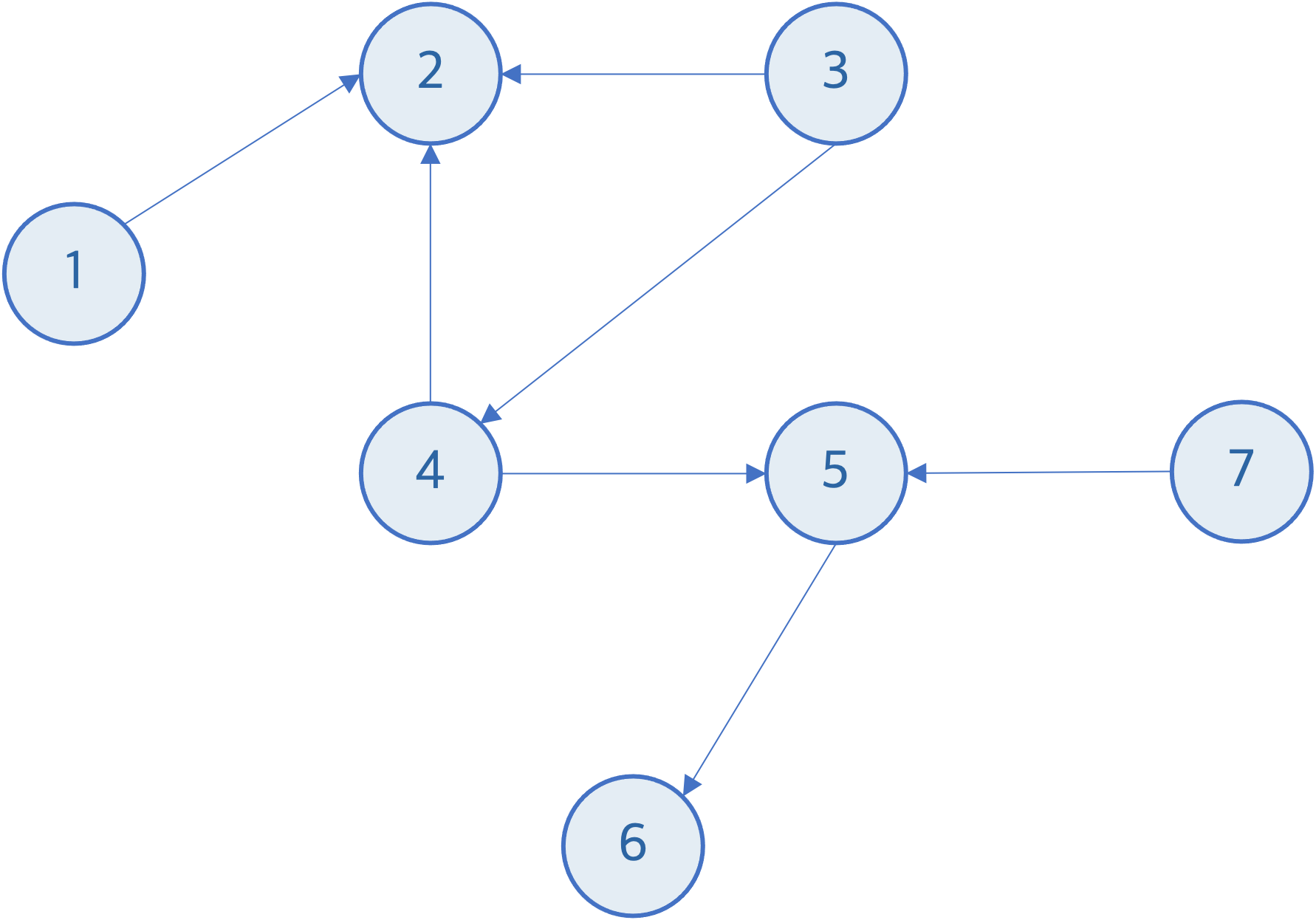
간선이 노드 x에서 노드 y로 흐를 때, 노드 x는 노드 y보다 앞에 위치되어야 한다.
- 즉, 어떠한 노드가 해당 노드 쪽으로 들어오는 간선을 가지고 있다면 이 노드는 가장 앞에 올 수 없다.
- 결과적으로, 현재 상태에서 가장 앞에 올 수 있는 노드들은 indegree(노드로 들어오는 간선의 수)가 0인 노드들이다.

위의 그래프에서 각 노드들의 indegree들을 구해보면, 노드 1, 3, 7의 indegree가 0이다. queue에는 현재의 그래프에서 가장 앞에 위치할 수 있는 노드들의 후보를 담는다. 현재는 노드 1, 3, 7만이 가장 앞에 정렬될 수 있으므로 해당 노드들을 큐에 넣는다. 이후, 큐에 있는 후보들을 하나씩 꺼내 정렬 결과 벡터 result에 넣어주고, 해당 노드를 지운다.


result 벡터는 위상정렬의 최종 결과가 저장되는 배열이다. 큐의 가장 앞에 있는 노드 1을 result에 넣은 뒤, 노드 1을 그래프에서 지운다. 노드 1을 그래프에서 지울 때는 입력받은 graph 배열에서 지울 필요 없이 indegree 배열만 업데이트 하면 된다. 노드 1은 노드 2로 향하는 간선을 가지고 있으므로 노드 1을 지우면서 노드 2의 indegree 수를 1 감소 시킨다.
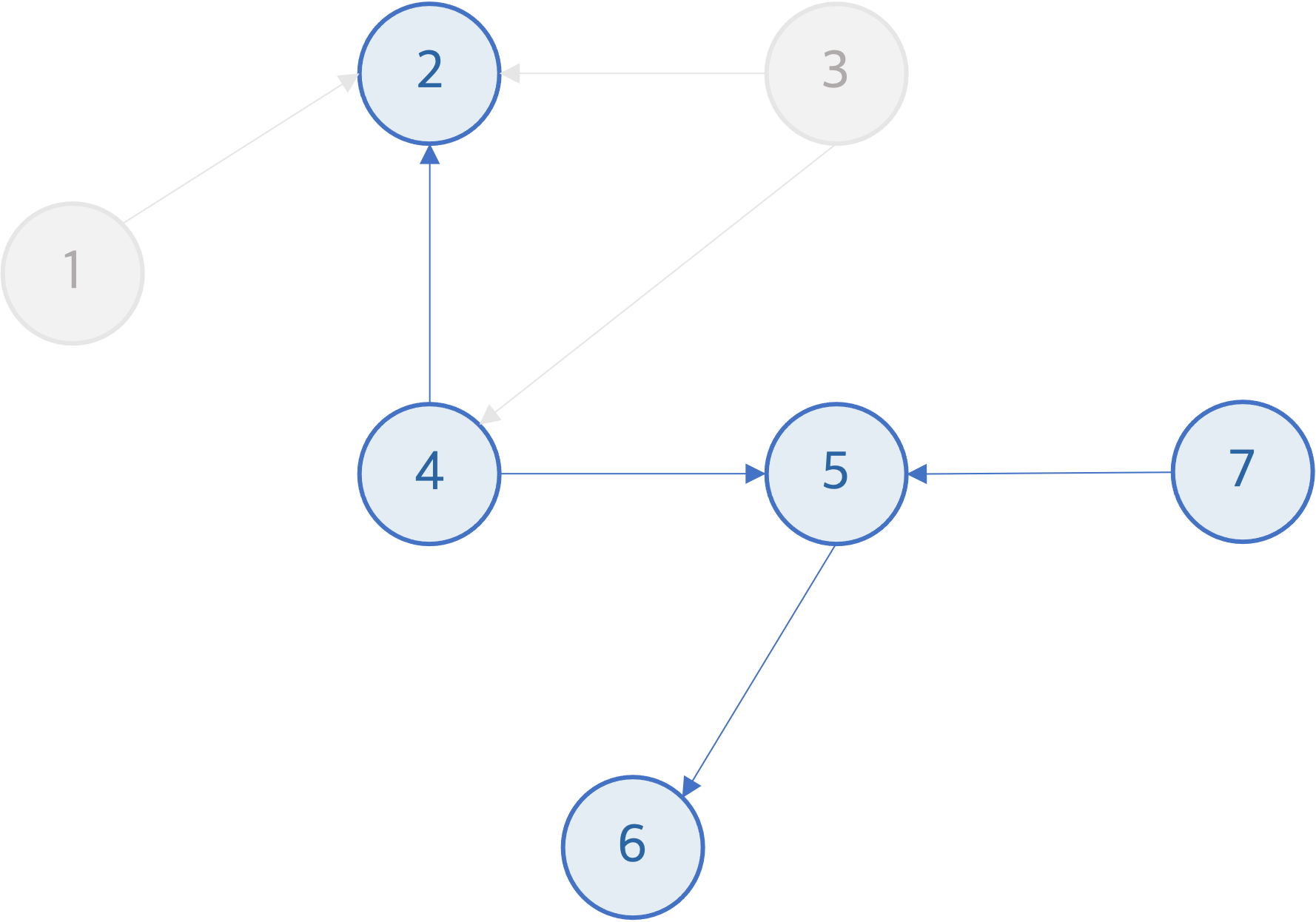

큐에서 노드 3을 꺼내 result 배열에 넣는다. 이후, 노드 3을 그래프에서 지운다. 노드 3은 노드 2와 노드 4를 가리키고 있으므로 노드 2와 노드 4의 indegree는 1개씩 줄어든다. 이 때, 노드 4번의 indegree가 0이 되므로 노드 4번 역시 현재 그래프에 남아있는 노드들 중 가장 앞에 위치 할 수 있다. 따라서 노드 4번을 큐에 추가한다.


큐에서 노드 7을 꺼내 result에 넣은 후 노드 7을 그래프에서 지운다. 노드 7은 노드 5를 가리키고 있으므로 노드 5의 indegree를 1 감소시킨다.
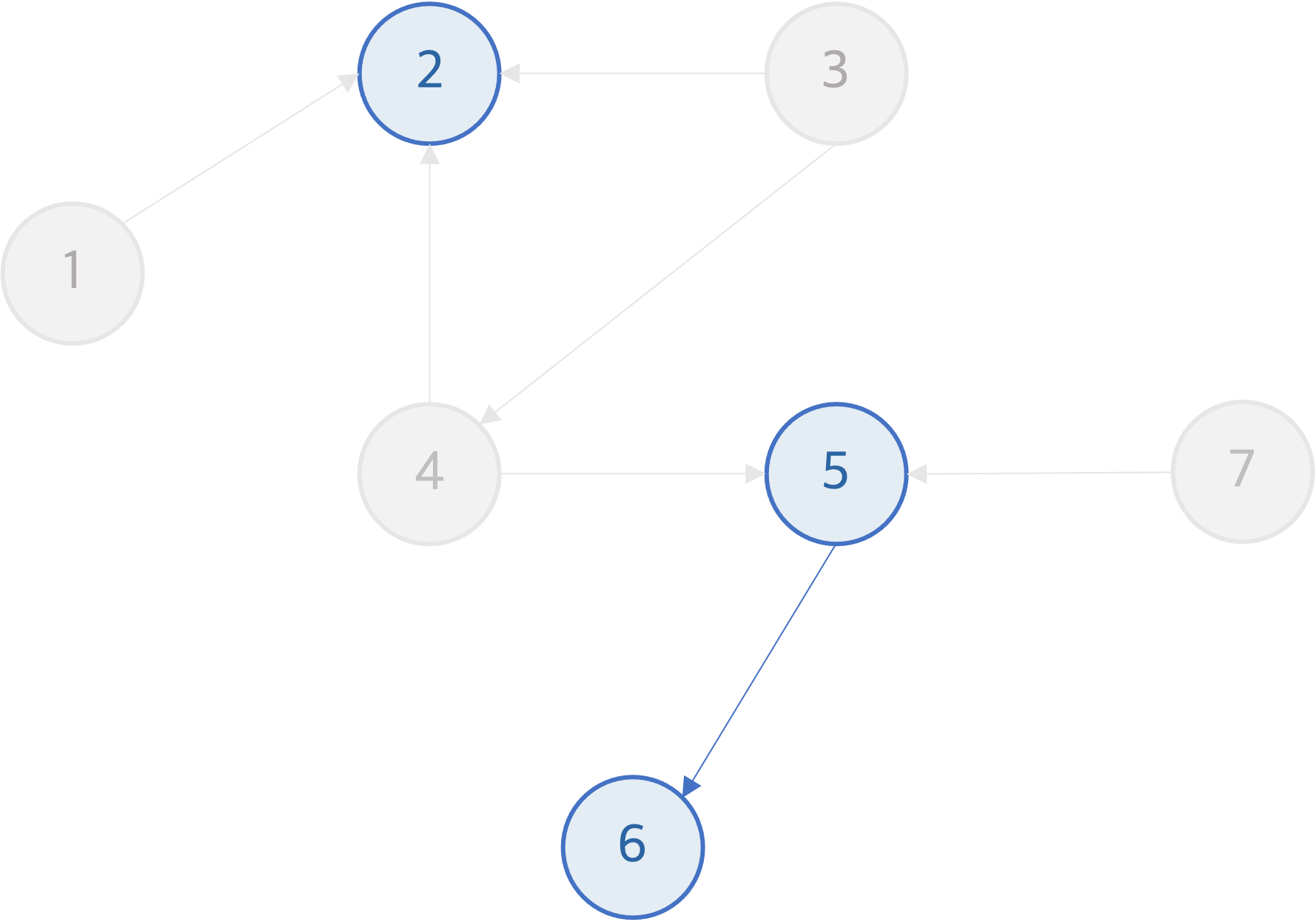
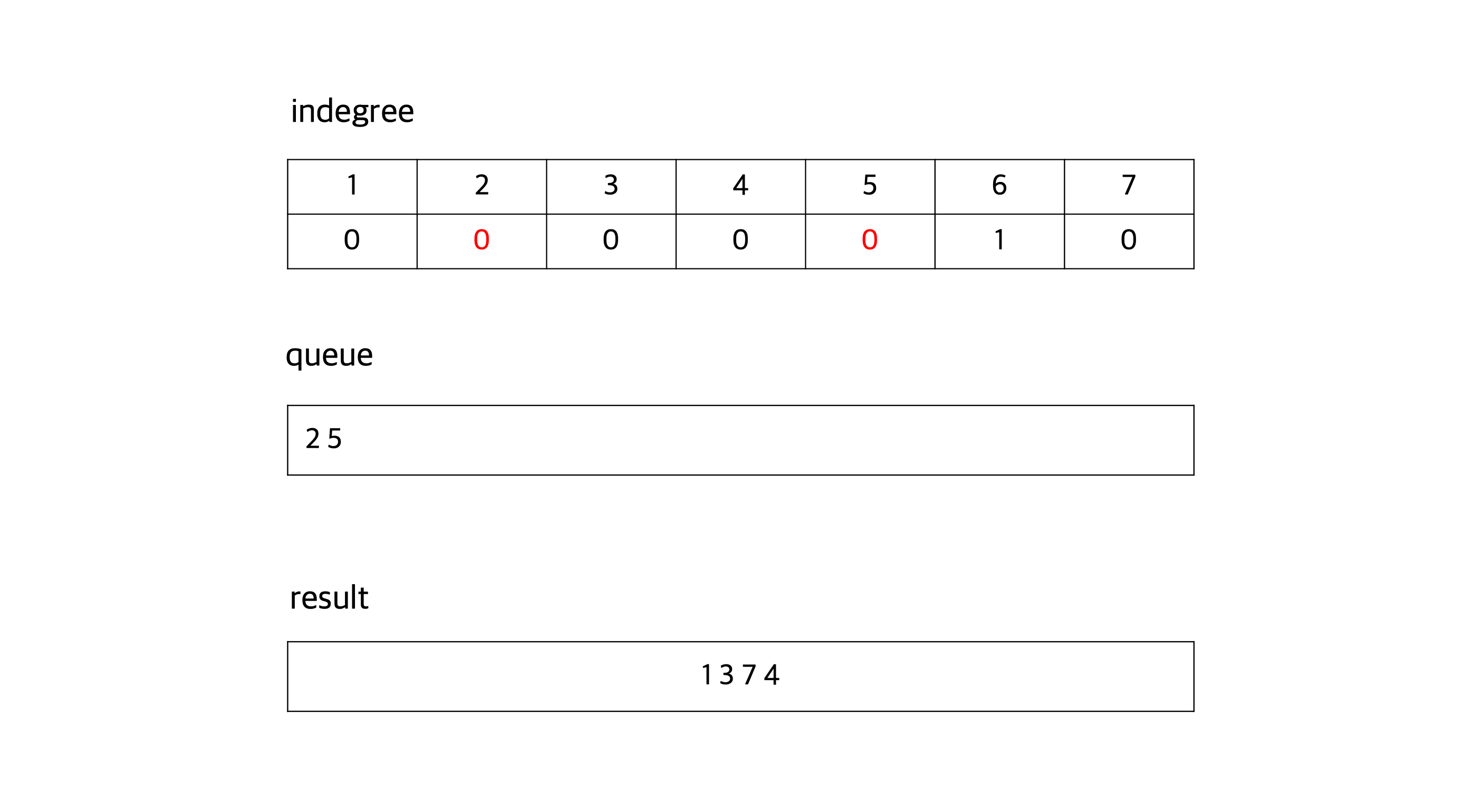
큐에서 노드 4를 꺼내 result에 넣은 후 노드 4를 그래프에서 지운다. 노드 4는 노드 2와 노드 5를 가리키고 있으므로 노드 2와 노드 5의 indegree를 1씩 감소시킨다. 노드 2와 노드 5의 indegree가 0이 된다. 노드 2와 노드 5는 그래프에 남아있는 노드들 중 가장 앞에 위치할 수 있으므로 이들을 큐에 넣는다.
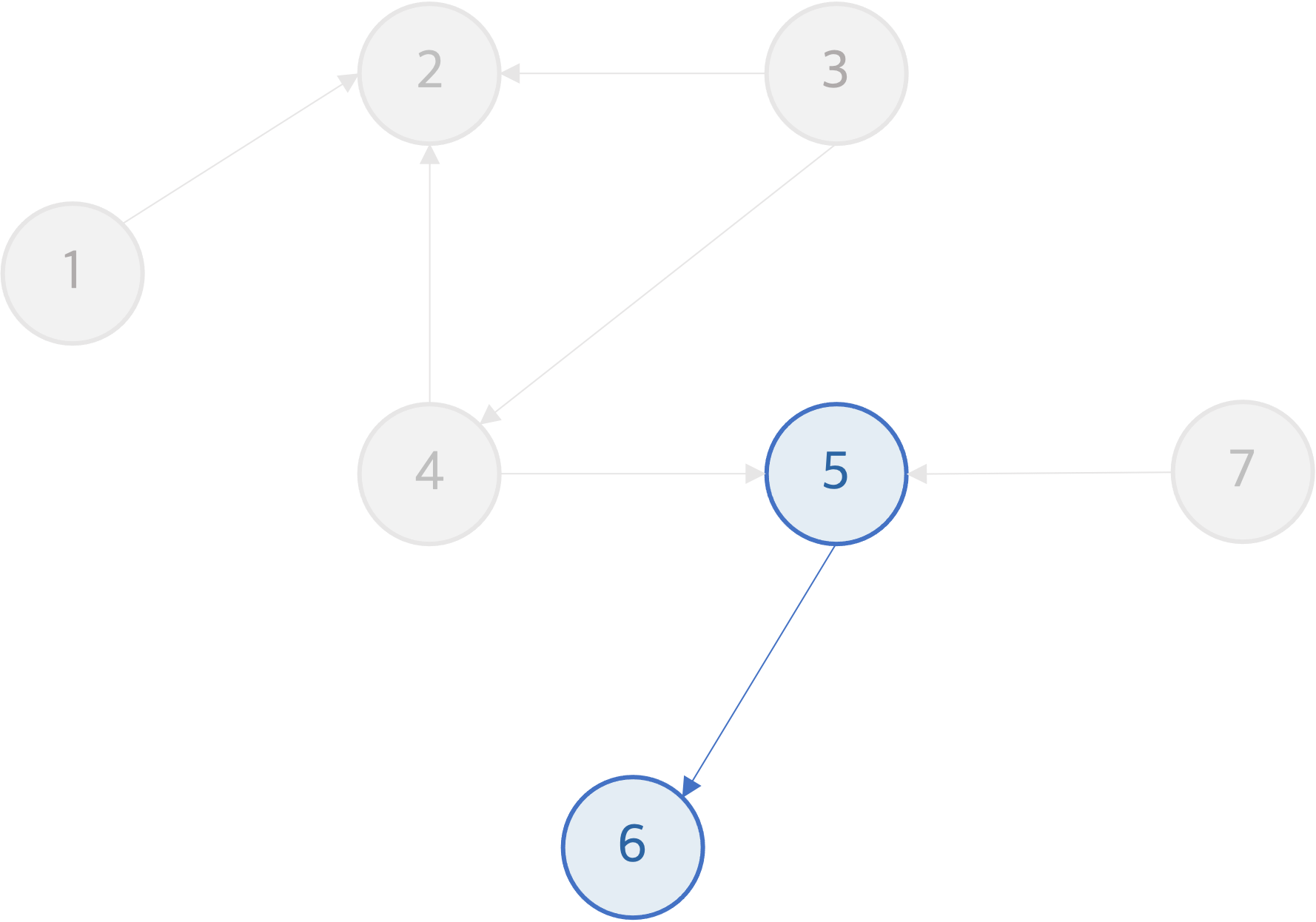
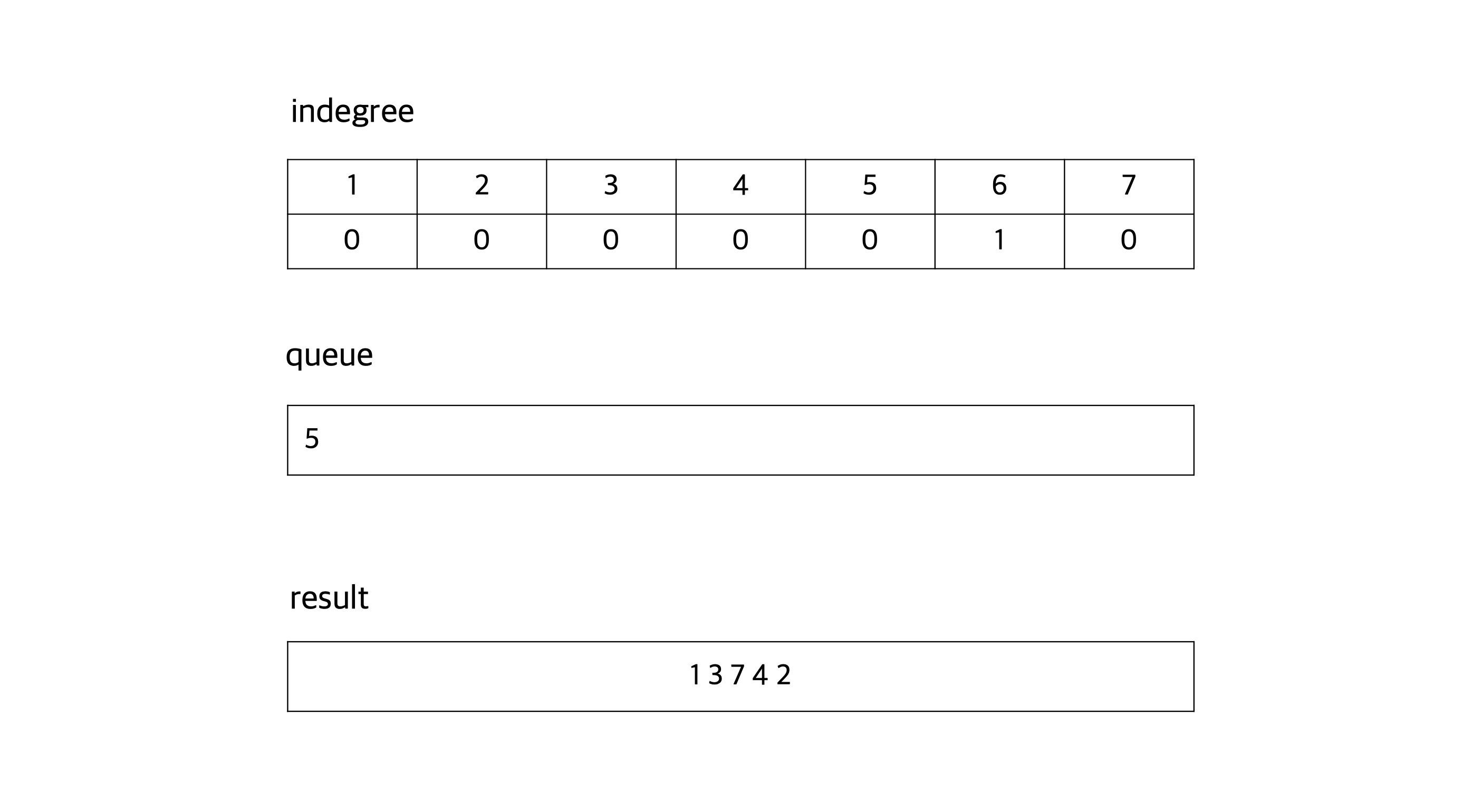
큐에서 노드 2를 꺼내 result에 넣고, 그래프에서 노드 2를 삭제한다.


큐에서 노드 5를 꺼내 result 배열에 넣고, 그래프에서 노드 5를 삭제한다. 노드 5는 노드 6을 가리키고 있으므로 노드 6의 indegree를 1감소시킨다. 이 때, 노드 6의 indegree는 0이 된다.노드 6은 현재 그래프에 남아있는 노드들 중 노드 6이 가장 앞에 위치할 수 있다.

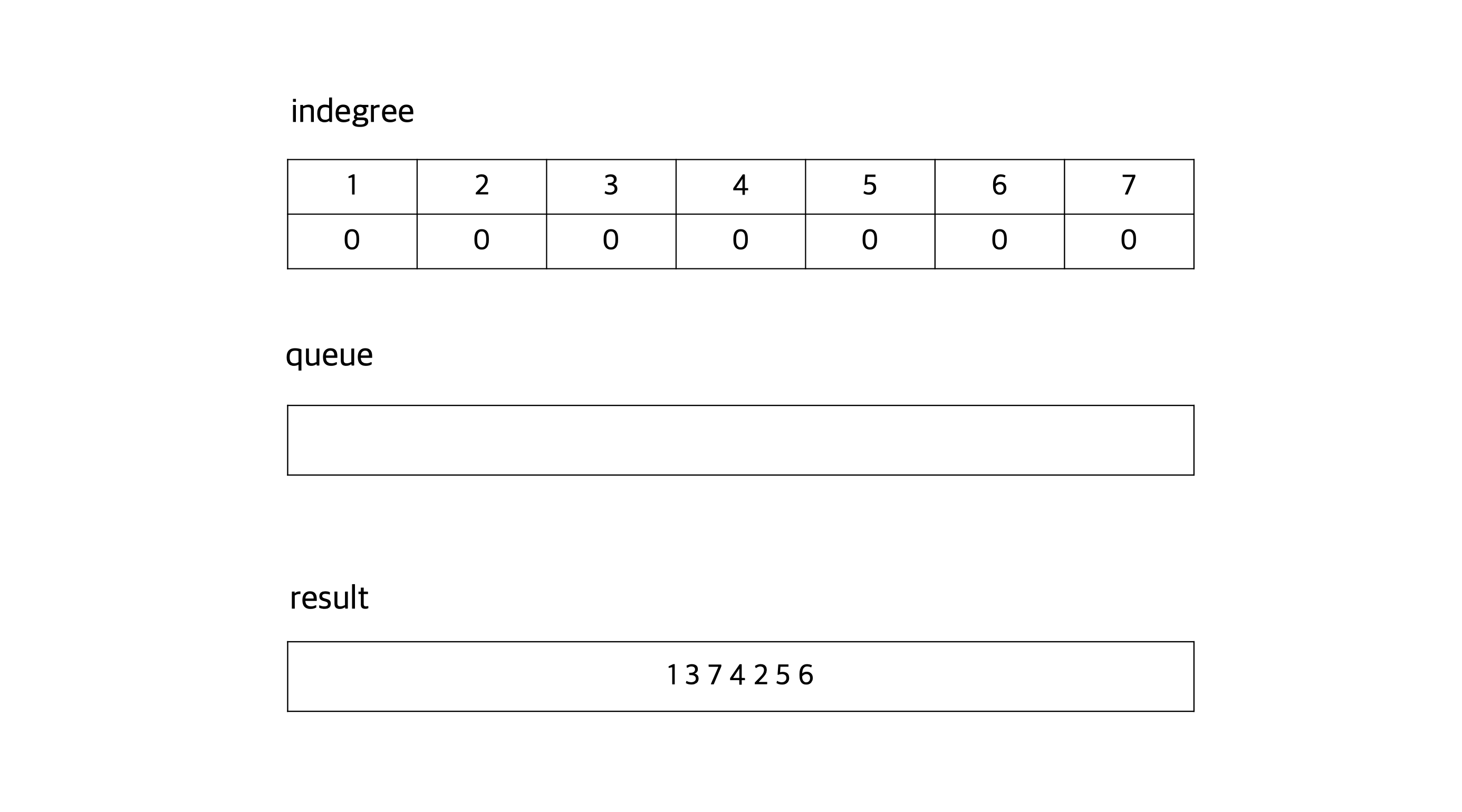
최종적으로 그래프에 있는 노드를 모두 지우면, result에 위상 정렬한 결과가 저장된다.
사이클이 있는 그래프에서 위상정렬을 수행한 경우 result에 N개의 노드가 모두 저장되지 않는다. 따라서 result.size()를 통해 사이클이 있는 그래프였는지 확인이 가능하다.
위상정렬의 시간복잡도는 O(V+E)이다.
(V는 정점의 수, E는 간선의 수)
전체 코드
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
int N, M;
vector<int> result;
vector<int> indegree(1000);
vector<vector<int>> graph(1000, vector<int>(0));
void setGraph() {
scanf("%d %d", &N, &M);
for (int i=0; i<M; i++) {
int u, v;
scanf("%d %d", &u, &v);
graph[u].push_back(v);
indegree[v]++;
}
}
void topologicalSort() {
queue<int> q;
for (int i=1; i<=N; i++) {
if (!indegree[i]) q.push(i);
}
while (!q.empty()) {
int cur = q.front();
q.pop();
result.push_back(cur);
for (int i=0; i<graph[cur].size(); i++) {
int next = graph[cur][i];
indegree[next]--;
if (!indegree[next]) q.push(next);
}
}
}
int main() {
setGraph();
topologicalSort();
if (result.size() == N) {
for (auto x : result) printf("%d ", x);
}
else printf("Cycled graph.");
return 0;
}
/*
input:
7 7
1 2
4 2
3 2
3 4
4 5
7 5
5 6
output:
1 3 7 4 2 5 6
*/'Computer Basics > Algorithm Techniques' 카테고리의 다른 글
| 최소신장트리(Minimal Spanning Tree)_크루스칼(Kruscal) 알고리즘 (0) | 2022.03.04 |
|---|---|
| 유니온파인드(Union-Find) (0) | 2022.03.03 |
| 트리_그래프가 트리인지 확인하는 방법 (0) | 2022.02.28 |
| 이진트리순회_레벨순회(level)/전위순회(preorder)/중위순회(inorder)/후위순회(postorder) (0) | 2022.02.27 |
| 가장긴증가하는부분수열(LIS)_DP/Binary Search (0) | 2022.02.20 |
댓글