Union-Find 에 대한 이해
- 공통 원소가 없는, "상호 배타적"인 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조이다.
- 원소들이 어떠한 집합에 포함되어있을 때, 특정 원소가 포함되어있는 집합을 찾는 Find 연산을 지원한다.
- 두 원소들이 속한 집합이 다를 때, 두 집합을 하나의 집합으로 합치는 Union 연산을 지원한다.
트리 형태로 표현되어있는 원소들간의 서로소 집합을 살펴보자.
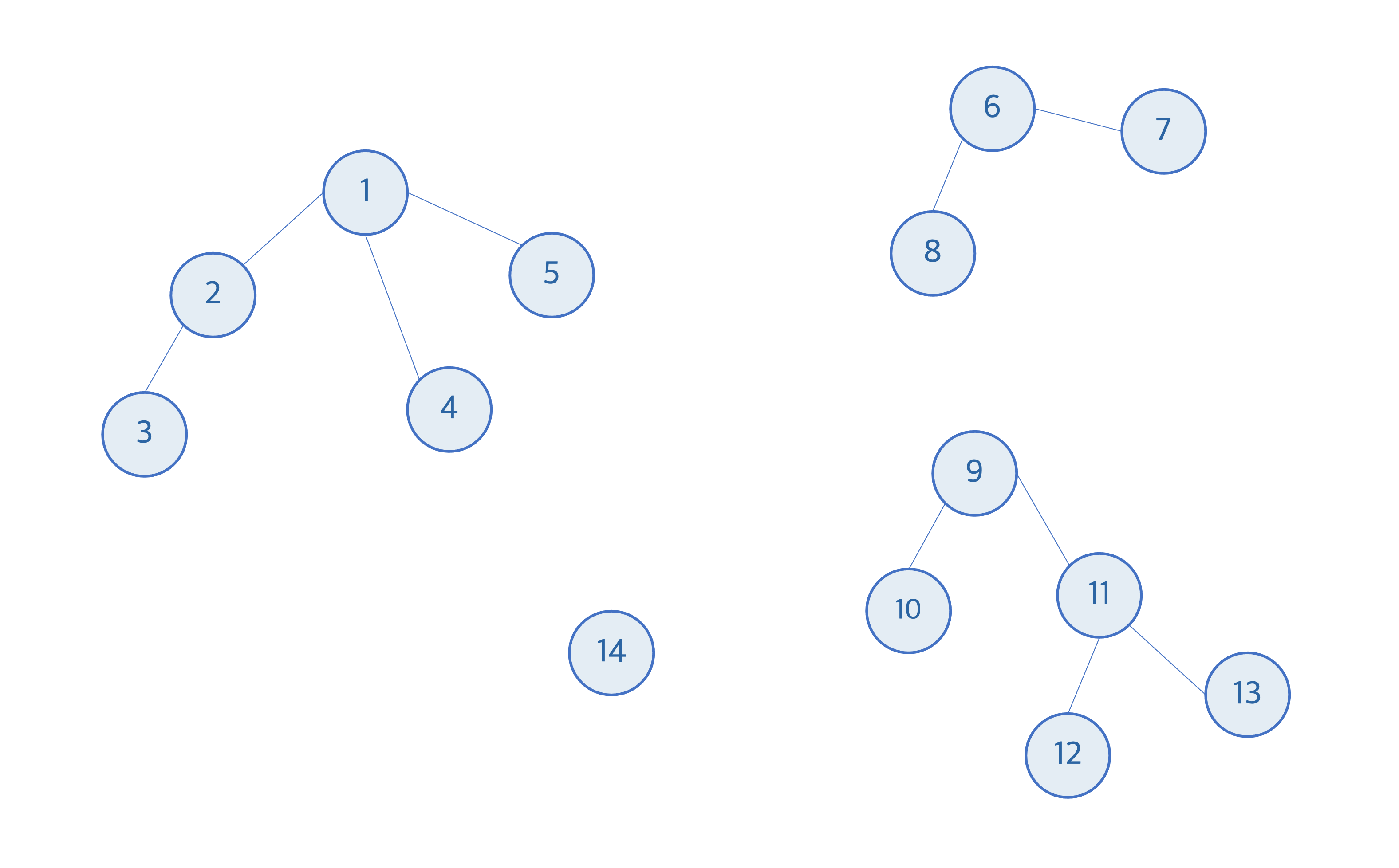
위의 그림에서 원소들의 상호 배타적 집합은 총 4개이다. 각 원소들은 하나의 집합에 포함되어있고, 같은 집합에 포함되어있는 원소들은 같은 루트 노드를 공유한다. 예를 들어, 노드 2번과 노드 4번은 같은 집합에 포함되어 하나의 트리로 연결되어있고 루트 노드 1번을 공유한다. 노드 6번과 노드 11번은 각각 다른 집합에 포함되어있고 다른 루트노드를 가진다. 노드 14번은 자체의 집합이면서, 자체의 루트 노드를 가진다.
Find 연산은, 어떠한 노드가 주어졌을 때 그 노드가 속한 집합을 찾는다. 각 집합은 루트 노드의 번호를 대표로 사용할 수 있으므로 집합의 루트 노드를 반환한다. 예를 들어, 노드 10에 find 연산을 수행할 경우, 노드 10이 속해있는 집합의 루트 노드 번호 9를 반환한다.
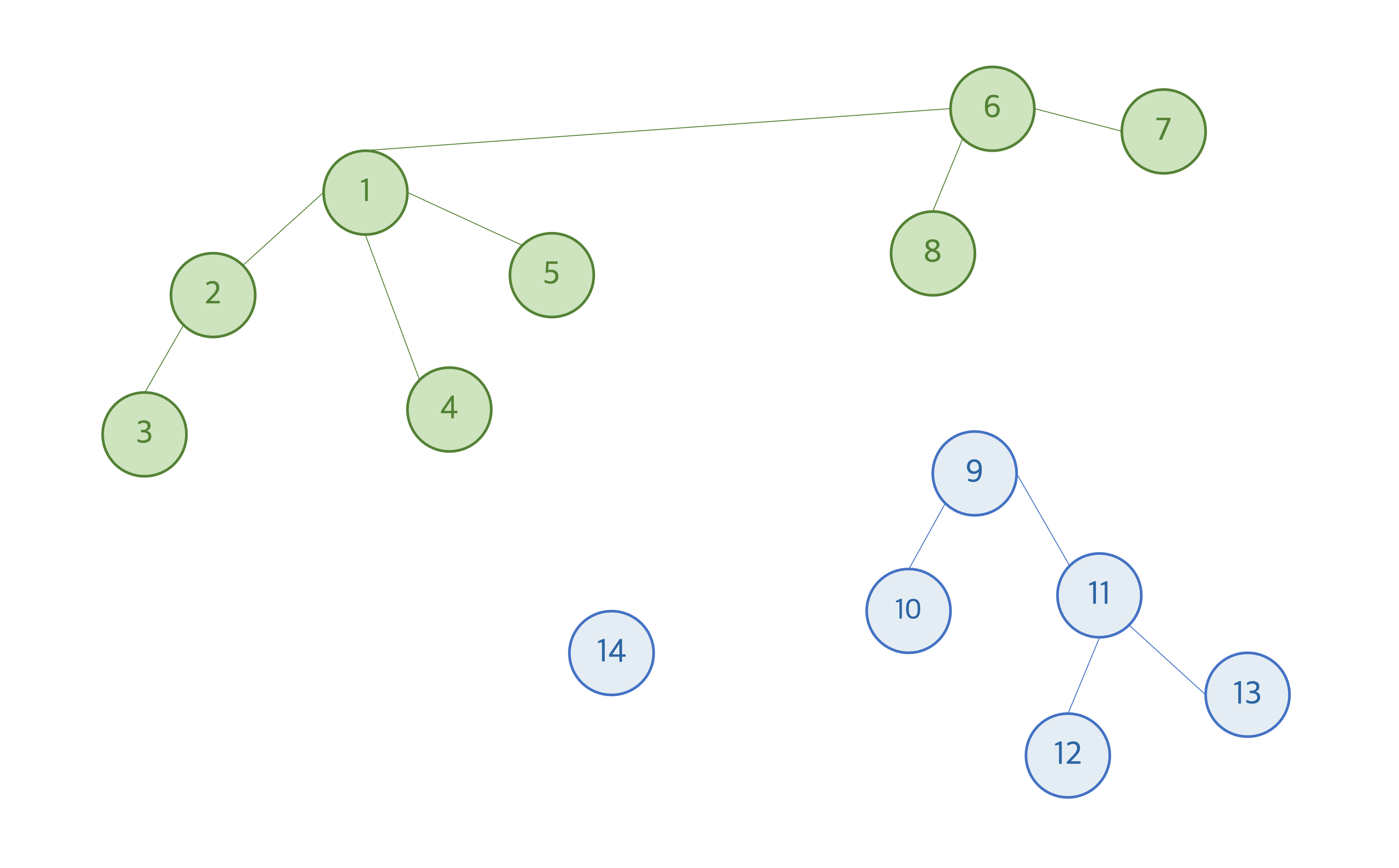
union 연산은, 두 노드가 주어졌을 때 두 노드가 속한 집합을 각각 찾고, 해당 집합들을 합치는 연산이다. 예를 들어 노드 2번과 노드 6번에 union 연산을 수행하였을 경우, 노드 2가 속해있는 루트 1번의 집합과 노드 6이 속해있는 루트 6번의 집합을 합쳐 연결한다.
Union-Find 의 구현
- 초기화: N개의 원소가 각자 다른 집합으로 존재하도록 초기화한다. 이 떄, 각 노드들의 부모 노드는 자기 자신이 된다.
- find(int u): 정점 u가 속한 트리의 루트 노드를 찾는다. 해당 정점이 트리의 루트인 경우 정점 번호를 리턴한다. 해당 정점이 트리의 루트가 아니라면, 재귀적으로 부모 노드를 타고 올라가 루트 노드를 찾는다.
- union(int u, int v): find 연산을 통해 정점 u와 정점 v의 루트 노드를 찾는다. 만약 두 원소의 루트 노드가 다르면 이들은 다른 집합에 속한 것이므로 두 집합을 합친다.
#include <vector>
#include <iostream>
using namespace std;
int N = 10;
vector<int> parent(10, 0);
// 초기화: 모든 정점이 다른 집합에 존재하도록 설정
void initialize() {
for (int i=1; i<=N; i++)
parent[i] = i;
}
// find: 정점 u의 루트 노드를 반환
int find(int u) {
if (parent[u] == u) return u;
return find(parent[u]);
}
// merge(union): 정점 u와 정점 v가 속한 집합이 다른 경우, 두 집합을 합함
void merge(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ; // 속한 집합이 같다면 합칠 필요 없음
parent[u] = v;
}
int main() {
initialize();
merge(1, 2);
merge(2, 3);
merge(3, 4);
merge(4, 5);
merge(5, 6);
merge(6, 7);
merge(7, 8);
merge(8, 9);
merge(9, 10);
for (int i=1; i<=N; i++) cout<<parent[i]<<" ";
cout<<endl;
return 0;
}
Union-Find 의 최적화: Union-Find by Rank
union(merge) 함수의 시간복잡도는 find 연산의 시간복잡도에 비례한다. find 연산은 트리의 부모 노드들을 타고 올라가 루트 노드를 찾는 연산이므로, 원소가 속한 트리의 높이에 비례한다.
따라서, 다음 그림과 같이 정점들이 연결되는 경우 트리의 높이는 N이 되어 최악의 시간복잡도는 O(N)이 된다.

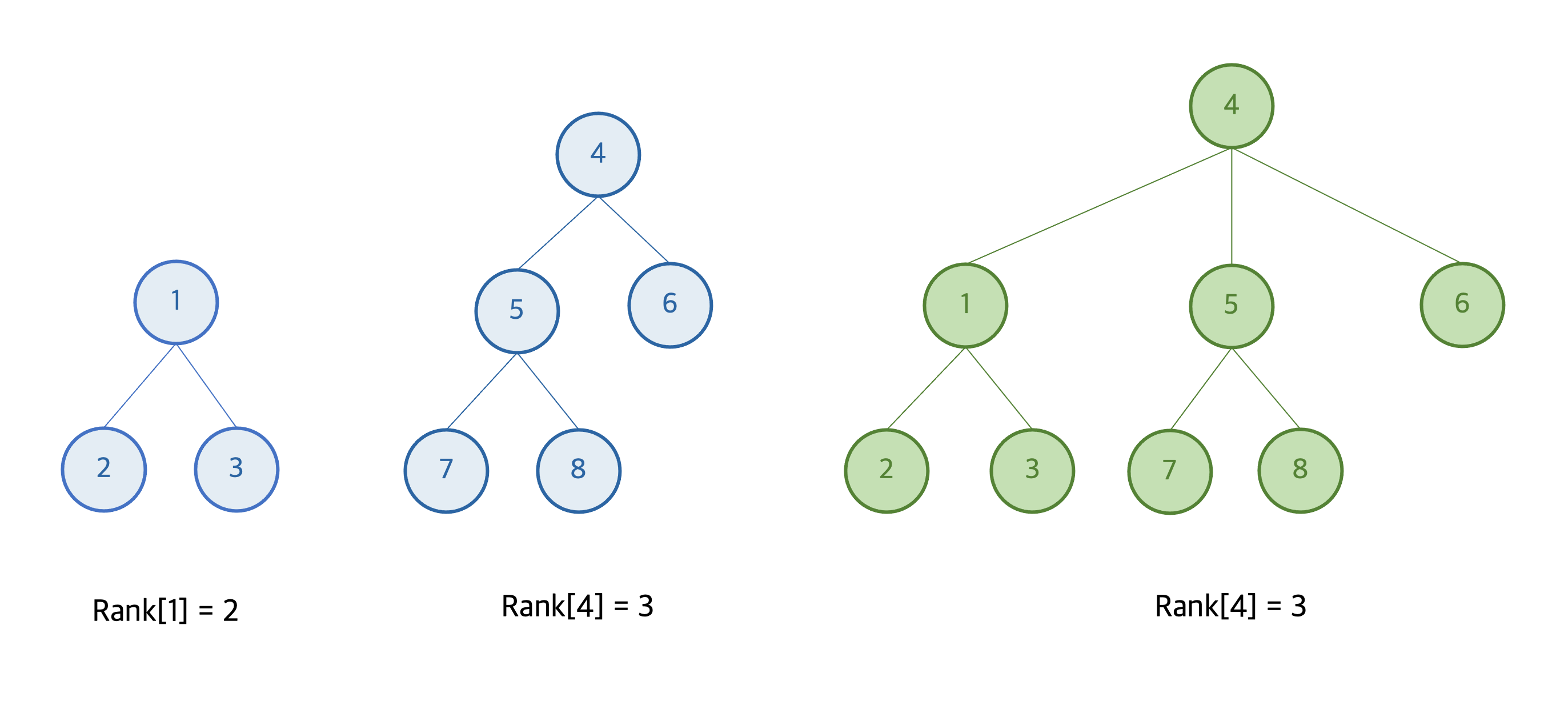
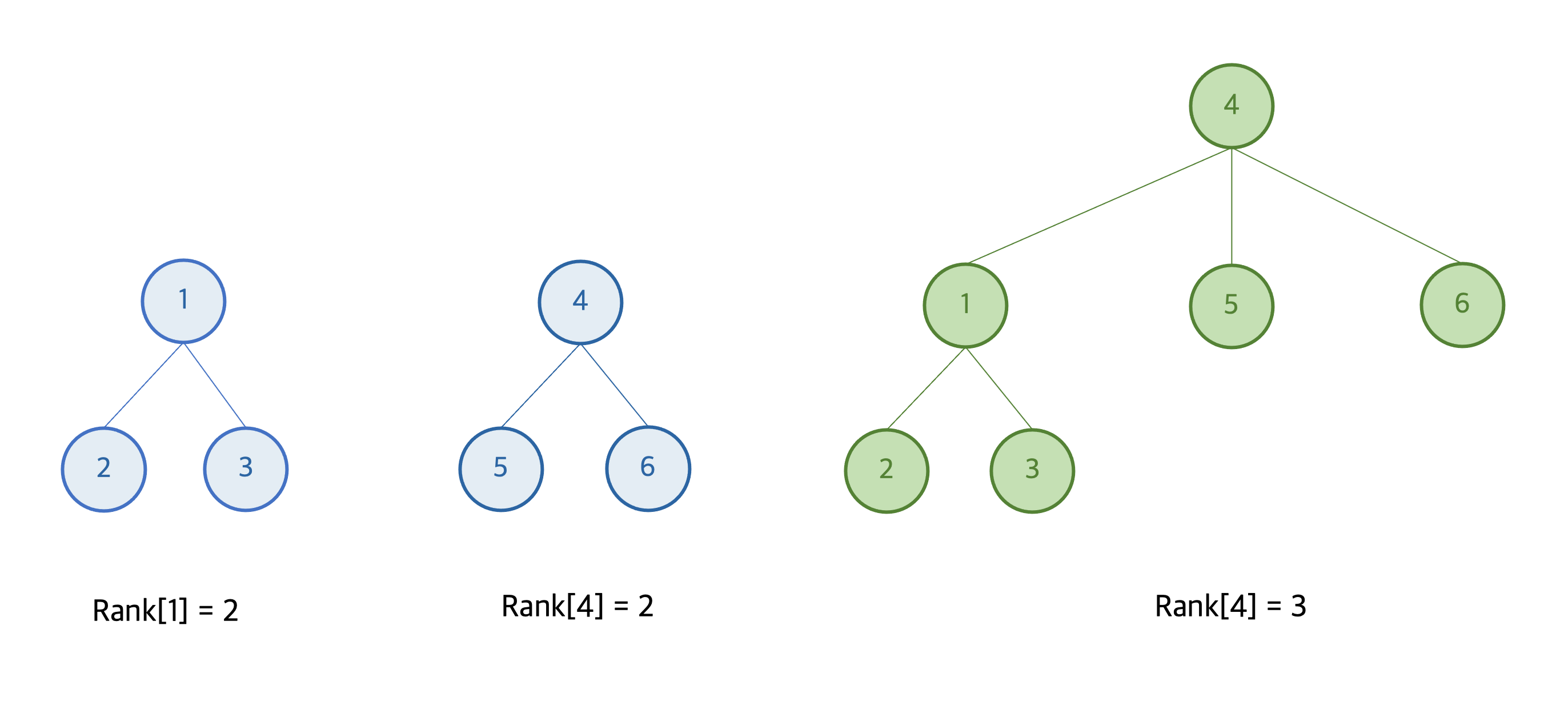
이러한 상황을 막기 위해, 높이(rank)가 낮은 트리를 높이가 높은 트리의 밑에 넣는 union-by-rank 방법을 사용할 수 있다. 높이가 낮은 트리를 높이가 높은 트리의 밑에 넣으면, 두 트리의 높이가 다를 경우 합친 트리의 높이는 변함이 없고, 합치고자 하는 두 트리의 높이가 같을 경우에만 합친 트리의 높이가 1 증가한다. 결국, 트리의 높이는 노드 개수의 log에 비례하게 되고,시간복잡도 O(logN) 내에 Union-Find 알고리즘을 수행할 수 있게 된다.
전체 코드
#include <vector>
#include <iostream>
using namespace std;
int N = 10;
vector<int> nrank(10, 1);
vector<int> parent(10, 0);
// 초기화: 모든 정점이 다른 집합에 존재하도록 설정
void initialize() {
for (int i=1; i<=N; i++)
parent[i] = i;
}
// find: 정점 u의 루트 노드를 반환
// 경로 압축을 위해 재귀적으로 구한 루트 노드 번호를 parent[u]에 저장
int find(int u) {
if (parent[u] == u) return u;
return parent[u] = find(parent[u]);
}
// merge(union): 정점 u와 정점 v가 속한 집합이 다른 경우, 두 집합을 합함
void merge(int u, int v) {
u = find(u);
v = find(v);
// 속한 집합이 같다면 합칠 필요 없음
if (u == v) return ;
// 높이(nrank)가 더 큰 트리의 루트 노드를 v에 저장
if (nrank[u] > nrank[v]) swap(u, v);
// 높이가 낮은 트리를 높이가 높은 트리에 연결
parent[u] = v;
// 두 트리의 높이가 같다면 결과 트리의 높이를 1 증가
if (nrank[u] == nrank[v]) nrank[v]++;
}
int main() {
initialize();
merge(1, 2);
merge(2, 3);
merge(3, 4);
merge(4, 5);
merge(5, 6);
merge(6, 7);
merge(7, 8);
merge(8, 9);
merge(9, 10);
for (int i=1; i<=N; i++) cout<<parent[i]<<" ";
cout<<endl;
return 0;
}
Union-Find 시간복잡도
경로 압축, Union-Find by rank 등의 최적화 과정을 모두 수행하였을 때, 시간 복잡도는 O(a(N))이다. 이는, 에커먼 함수에 의해 정의되는 것으로, 모든 N에 대해 현실적으로 4 이하의 값을 갖는다. 따라서, 최적화를 진행한 Union-Find 알괴즘의 시간복잡도는 아주 작은 상수로 취급할 수 있다.
'Computer Basics > Algorithm Techniques' 카테고리의 다른 글
| 최단거리구하기_플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2022.03.07 |
|---|---|
| 최소신장트리(Minimal Spanning Tree)_크루스칼(Kruscal) 알고리즘 (0) | 2022.03.04 |
| 위상정렬(Topological sort) (0) | 2022.03.01 |
| 트리_그래프가 트리인지 확인하는 방법 (0) | 2022.02.28 |
| 이진트리순회_레벨순회(level)/전위순회(preorder)/중위순회(inorder)/후위순회(postorder) (0) | 2022.02.27 |
댓글