퀵 정렬에 대한 이해
- 퀵 정렬이란, 피벗을 설정하여 이를 올바른 위치로 이동시킨 뒤 나머지 원소들을 두 개의 배열로 분할하여 재귀적으로 정렬시키는 알고리즘이다.
- 합병정렬과 달리, 배열이 불균등하게 분할된다.(운이 좋으면, 균등하게 분할 될 수도 있다.)
코드를 먼저 보면,
void quickSort(int st, int en) {
if (en <= st+1) return ;
// 피벗을 올바른 위치로 이동시키기
int pivot = arr[st];
int l = st+1; //왼쪽에서 오른쪽으로 이동
int r = en-1; //오른쪽에서 왼쪽으로 이동
while (1) {
while (l <= r && arr[l] <= pivot) l++;
while (l <= r && arr[r] >= pivot) r--;
if (l > r) break;
swap(arr[l], arr[r]);
}
swap(arr[st], arr[r]);
//배열을 두 배열로 분할하여 재귀적으로 정렬
quickSort(st, r);
quickSort(r+1, en);
}
퀵 정렬은 두가지 부분으로 이루어진다.
첫째는 pivot을 설정하고 이를 올바른 위치로 이동시키는 부분이다. pivot이 올바른 위치에 있다는 것은 pivot의 앞쪽에 pivot보다 작거나 같은 수들만 존재하고 pivot의 뒤쪽에 pivot보다 크거나 같은 수들만 존재한다는 의미이다.
예를 들어, N= 8 인 다음과 같은 배열을 정렬시킬 때 pivot을 가장 처음 수로 지정한다면,

pivot의 올바른 위치는 인덱스 4번이 된다. 이전의 원소들과 이후 원소들의 순서는 상관 없으나, pivot 값인 5 앞에는 5보다 작거나 같은 수들만, 5 뒤에는 5보다 크거나 같은 수들만 존재할 수 있다.
둘째로, pivot을 제외한 나머지 원소들을 두가지 배열로 분할하여 재귀적으로 정렬시키는 부분이다. 피벗의 올바른 위치가 인덱스 r일 때, 전체 배열을 arr[st:r]과 arr[r:en]으로 분할하고, 각각의 배열을 정렬하여 최종 정렬을 완성한다.
Pivot을 올바르게 위치시키는 세부 과정
pivot을 올바르게 위치시키는 과정은 다음과 같다.

먼저, pivot = arr[st], l = st+1, r = en-1으로 설정한다. l은 왼쪽에서 오른쪽으로, r은 오른쪽에서 왼쪽으로 이동하는 포인터이다.

arr[l]이 pivot보다 작거나 같을 때까지 l을 오른쪽으로 이동시킨다. arr[r]이 pivot보다 크거나 같을 때까지 r을 왼쪽으로 이동시킨다.

인덱스 l과 r에 있는 원소들을 swap() 함수를 이용하여 교환한다.

arr[l]이 pivot보다 작거나 같을 때까지 l을 오른쪽으로 이동시킨다. arr[r]이 pivot보다 크거나 같을 때까지 r을 왼쪽으로 이동시킨다.

인덱스 l과 r에 있는 원소들을 swap() 함수를 이용하여 교환한다.

arr[l]이 pivot보다 작거나 같을 때까지 l을 오른쪽으로 이동시킨다. arr[r]이 pivot보다 크거나 같을 때까지 r을 왼쪽으로 이동시킨다. 인덱스 r과 l이 교차(r < l)하므로 반복문을 종료시킨다. 이 때, r의 최종위치가 pivot이 들어가야 하는 올바른 위치이다. pivot은 arr[st]이므로 arr[st]와 arr[r]을 교환한다.
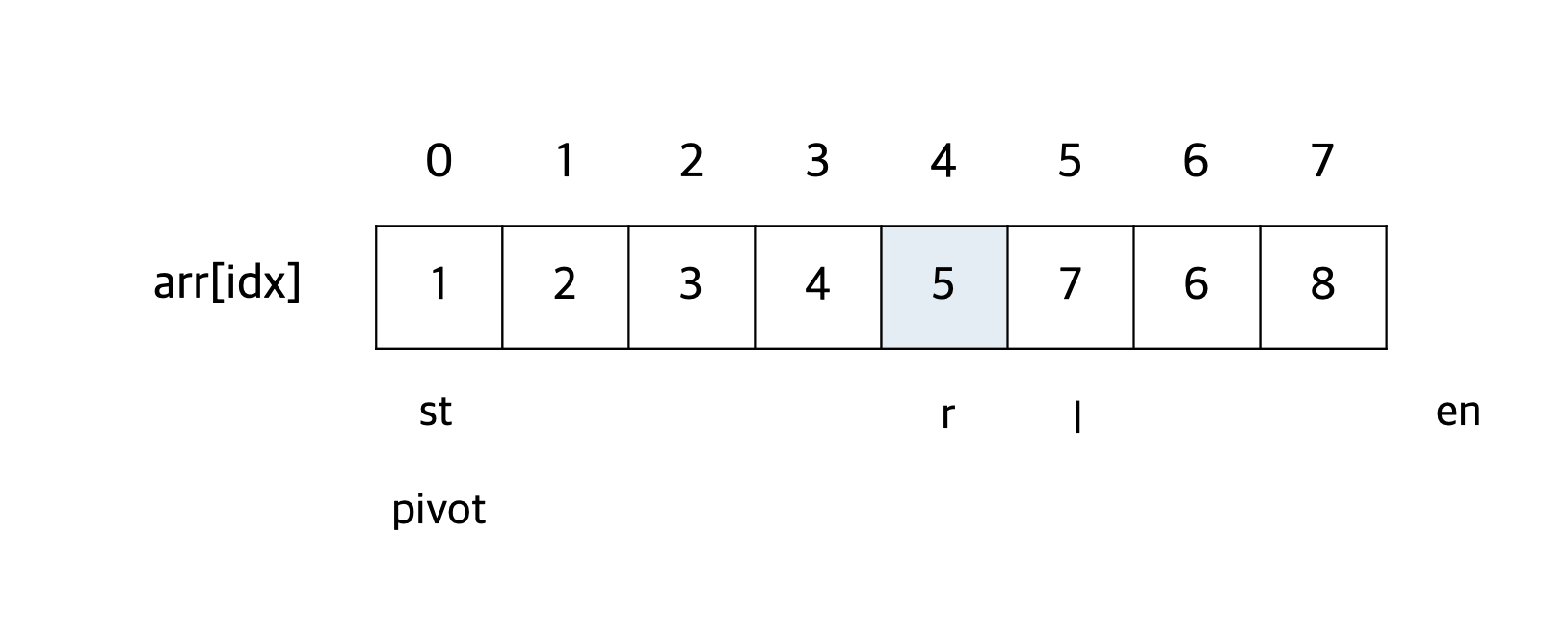
결과적으로, 5 앞에는 5보다 작거나 같은 수들만이, 5 뒤에는 5보다 크거나 같은 수들만이 위치하게 된다.
퀵 정렬의 시간복잡도
N = 2^k 개의 원소를 정렬한다고 가정할 때,
최선의 경우, 배열이 균등하게 이등분 되어 순환 호출의 깊이는 k가 된다. 각각의 단계에서 pivot을 올바르게 위치시키기 위한 비교 연산 횟수는 평균적으로 N번 이루어지므로 총 연산횟수는 O(kN)이다. 이때, k = logN 이므로 O(kN) = O(NlogN)이다.
베열이 이미 정렬되어있는 경우 최악의 시간복잡도를 가진다. 배열에서 원소가 한개씩만 분리되어 순환 호출의 깊이가 N이 된다. 각각의 단계에서 비교 연산이 평균적으로 N번 이루어지므로 총 연산횟수는 O(N^2)이다.
안정성과 제자리성
퀵 정렬은 정렬 후 동일한 원소에 대한 우선순위가 유지되지 않는다. 따라서 퀵 정렬은 불안정정렬(Unstable sort)이다. 기존 배열 이외의 추가적인 메모리를 거의 사용하지 않으므로 제자리정렬(In-place sort)이다.
전체 코드
#include <iostream>
using namespace std;
int N = 8;
int arr[8] = {3, 0, 2, 1, 6, 5, 4, 7};
void quickSort(int st, int en) {
if (en <= st+1) return ;
int pivot = arr[st];
int l = st+1; //왼쪽에서 오른쪽으로 이동
int r = en-1; //오른쪽에서 왼쪽으로 이동
while (1) {
while (l <= r && arr[l] <= pivot) l++;
while (l <= r && arr[r] >= pivot) r--;
if (l > r) break;
swap(arr[l], arr[r]);
}
swap(arr[st], arr[r]);
quickSort(st, r); //배열 분할
quickSort(r+1, en);
}
void printarr() {
for (int i=0; i<N; i++)
printf("%d ", arr[i]);
}
int main() {
quickSort(0, N);
printarr();
}
/*
output: 0 1 2 3 4 5 6 7
*/'Computer Basics > Algorithm Techniques' 카테고리의 다른 글
| 이진트리순회_레벨순회(level)/전위순회(preorder)/중위순회(inorder)/후위순회(postorder) (0) | 2022.02.27 |
|---|---|
| 가장긴증가하는부분수열(LIS)_DP/Binary Search (0) | 2022.02.20 |
| 합병정렬(Merge sort)_개념/시간복잡도/Stable/Not In-place (1) | 2022.02.19 |
| 최대공약수(GCD)_Euclidean, 최소공배수(LCM) (0) | 2022.02.15 |
| 삽입정렬(Insertion Sort) 개념/시간복잡도/Stable/In-place (0) | 2022.02.11 |
댓글