합병 정렬에 대한 이해
- 합병정렬이란, 하나의 배열을 두개의 균등한 배열로 분할하고 분할된 배열을 각각 정렬한 다음, 이를 다시 합하여 정렬을 완성하는 알고리즘이다.
- 합병정렬은 분할 정복의 일종으로, 하나의 큰 문제를 두개의 작은 문제로 분할하여 해결한 다음, 결과를 모아서 문제를 완전히 해결하는 전략이다.
코드를 먼저 살펴보면,
void mergeSort(int st, int en) {
if (en == st+1) return ;
int mid = (st+en)/2;
mergeSort(st, mid); //arr[st:en]을 두개의 균등한 배열로 분할하여 각각 정렬
mergeSort(mid, en);
merge(st, en); //정렬된 두개의 배열 arr[st:mid], arr[mid:en]을 다시 합하기
}
arr[st:en](en 미포함)을 정렬한다고 할 때, 이를 균등하게 분할하여 arr[st:mid]와 arr[mid:en]을 각각 정렬한다. 이후, 정렬된 두 배열을 다시 합치는 과정을 통해 정렬 결과를 완성한다. 정렬된 두 배열을 합치는 함수는 merge()로, arr[st:mid]와 arr[mid:en]이 각각 정렬된 상태에서 arr[st:en] 전체가 오름차순으로 정렬되도록 만든다. 이 때, 정렬된 결과를 임시배열에 저장하고 정렬이 완료된 후 원래의 배열로 이동(복사) 시킨다.
void merge(int st, int en) {
int mid = (st+en)/2;
int i = st, j = mid;
for (int k=st; k<en; k++) {
if (i >= mid) tmp[k] = arr[j++]; //왼쪽 배열에서 남은 원소가 더이상 없을 때
else if (j >= en) tmp[k] = arr[i++]; //오른쪽 배열에서 남은 원소가 더이상 없을 때
else if (arr[i] <= arr[j]) tmp[k] = arr[i++]; //비교 후 더 작은 것 선택
else tmp[k] = arr[j++];
}
for (int k=st; k<en; k++) arr[k] = tmp[k]; //임시 배열 tmp의 결과를 원래의 배열로 복사
}
결국, 하나의 배열을 정렬하고자 할 때 재귀적으로 부분배열을 정렬하며 결과가 완성된다.
합병 정렬의 과정과 시간복잡도
N = 8인 다음과 같은 배열을 정렬할 경우, 정렬과정은 다음과 같다.
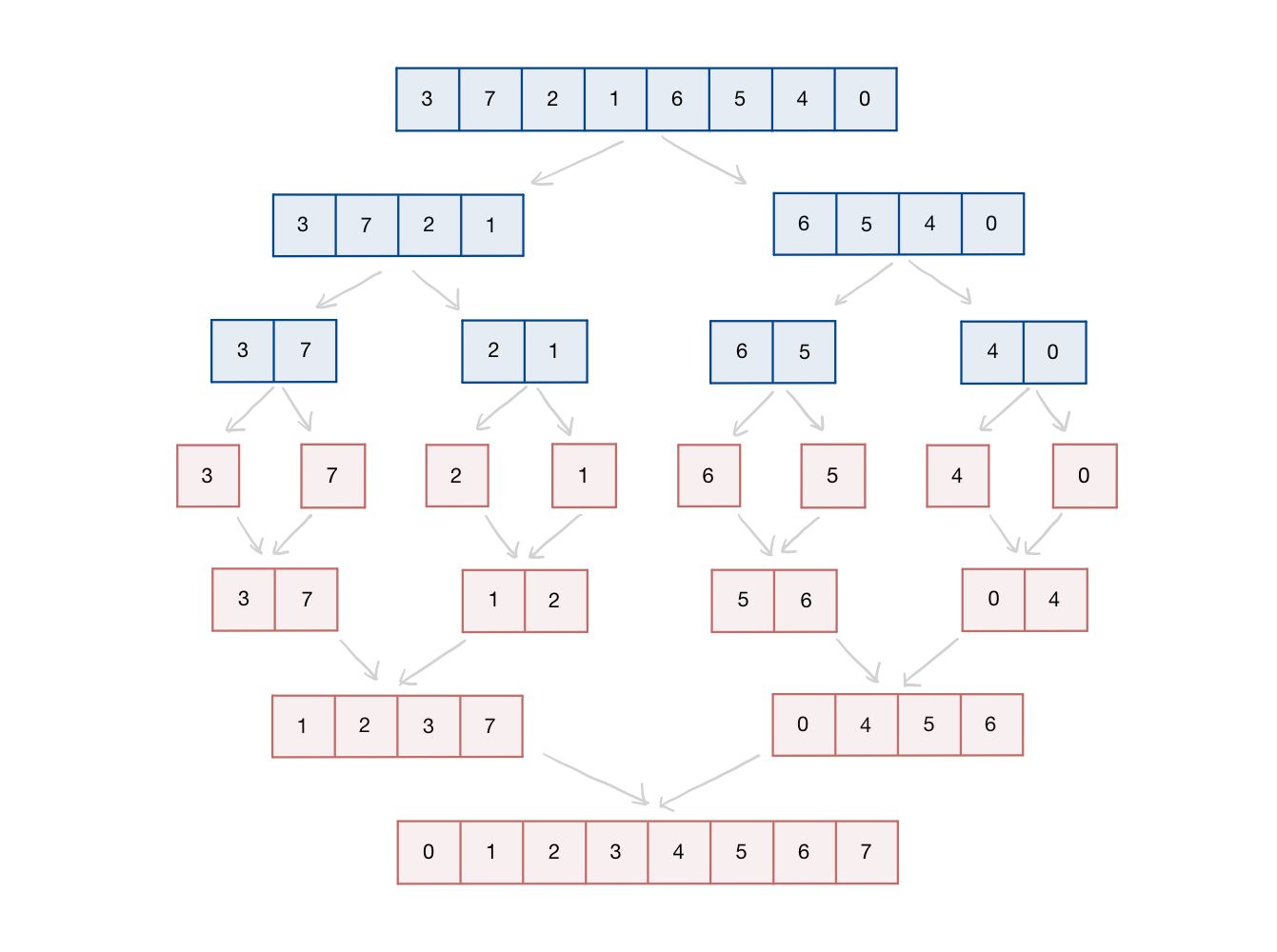
배열을 분할하는 과정에서는 별다른 비교연산이나 이동연산이 수행되지 않는다. 따라서, 분할된 결과들이 합병되는 과정에서의 비교, 이동 횟수를 살펴보면 된다.
배열의 길이를 N = 2^k 라 할 때, 합병 단계는 k번 일어난다. (위의 예시를 보면, N=2^3 이고, 합병 단계는 3번이라는 것을 확인할 수 있다.) 한번의 합병 단계에서는 여러번의 합병이 일어난다. (위의 예시를 보면, 1단계의 합병에서는 4번, 2단계의 합병에서는 2번, 3단계의 합병에서는 1번의 합병이 일어난다.) 한번의 합병이 일어날 때마다, 임시배열에 원소를 정렬하는 과정에서 원소 개수만큼의 비교연산이 수행된다. 또한, 임시배열의 원소를 원래의 배열로 이동시키는 과정에서 원소 개수만큼의 이동연산이 수행된다. 각각의 단계는 여러번의 합병을 포함하고 있으나, 결국 모든 원소들의 개수 합은 N개 이므로 각각의 단계에서 2N만큼의 이동,비교 연산이 일어난다. 결국, 시간복잡도는 합병 단계 k번 * 각각의 단계에서 연산 횟수 2N = O(kN)이 된다. N = 2^k, k = logN이므로 합병 정렬의 시간복잡도는 O(kN) = O(NlogN)이 된다.
안정성 & 제자리성
합병정렬 알고리즘으로 정렬을 수행하는 경우, 동일한 원소에 대하여 정렬 후 본래의 순서가 유지되기 때문에 안정정렬(Stable sort)이다. (정렬된 두 배열에 있는 원소들을 비교하는 과정에서 같으면 왼쪽에 있는 수를 먼저 가져오기 때문에 순서가 유지된다.) 다만, 정렬 과정에서 별도의 추가적인 메모리(임시배열)을 사용하므로 제자리정렬(In-place sort)가 아니다.
전체 코드
#include <iostream>
using namespace std;
int N = 8;
int arr[8] = {3, 7, 2, 1, 6, 5, 4, 0};
int tmp[100];
void merge(int st, int en) {
int mid = (st+en)/2;
int i = st, j = mid;
for (int k=st; k<en; k++) {
if (i >= mid) tmp[k] = arr[j++]; //왼쪽 배열에서 남은 원소가 더이상 없을 때
else if (j >= en) tmp[k] = arr[i++]; //오른쪽 배열에서 남은 원소가 더이상 없을 때
else if (arr[i] <= arr[j]) tmp[k] = arr[i++]; //원소들을 비교하여 더 작은 것 선택
else tmp[k] = arr[j++];
}
for (int k=st; k<en; k++) arr[k] = tmp[k]; //임시 배열 tmp의 결과를 원래의 배열로 복사
}
void mergeSort(int st, int en) {
if (en == st+1) return ;
int mid = (st+en)/2;
mergeSort(st, mid); //arr[st:en]을 두개의 균등한 배열로 분할하여 각각 정렬
mergeSort(mid, en);
merge(st, en); //정렬된 두개의 배열 arr[st:mid], arr[mid:en]을 다시 합하기
}
void printarr() {
for (int i=0; i<N; i++)
printf("%d ", arr[i]);
}
int main() {
mergeSort(0, N);
printarr();
}
/*
output: 0 1 2 3 4 5 6 7
*/'Computer Basics > Algorithm Techniques' 카테고리의 다른 글
| 가장긴증가하는부분수열(LIS)_DP/Binary Search (0) | 2022.02.20 |
|---|---|
| 퀵 정렬(Quick sort)_개념/시간복잡도/Unstable/In-place (0) | 2022.02.19 |
| 최대공약수(GCD)_Euclidean, 최소공배수(LCM) (0) | 2022.02.15 |
| 삽입정렬(Insertion Sort) 개념/시간복잡도/Stable/In-place (0) | 2022.02.11 |
| 버블정렬(Bubble sort) 개념/시간복잡도/Stable/In-place (0) | 2022.02.11 |
댓글