선택정렬에 대한 이해
- 선택 정렬이란, N-1번부터 1번까지의 자리에 대하여 해당 자리에 넣어야 하는 원소를 선택하는 알고리즘이다.
- 오름차순으로 정렬한다면, N-1번부터 1번까지의 자리에는 남아있는 수들 중 가장 큰 수를 선택하여 넣어야 한다.
N = 8인 다음과 같은 수열을 오름차순으로 정렬한다고 할 때,
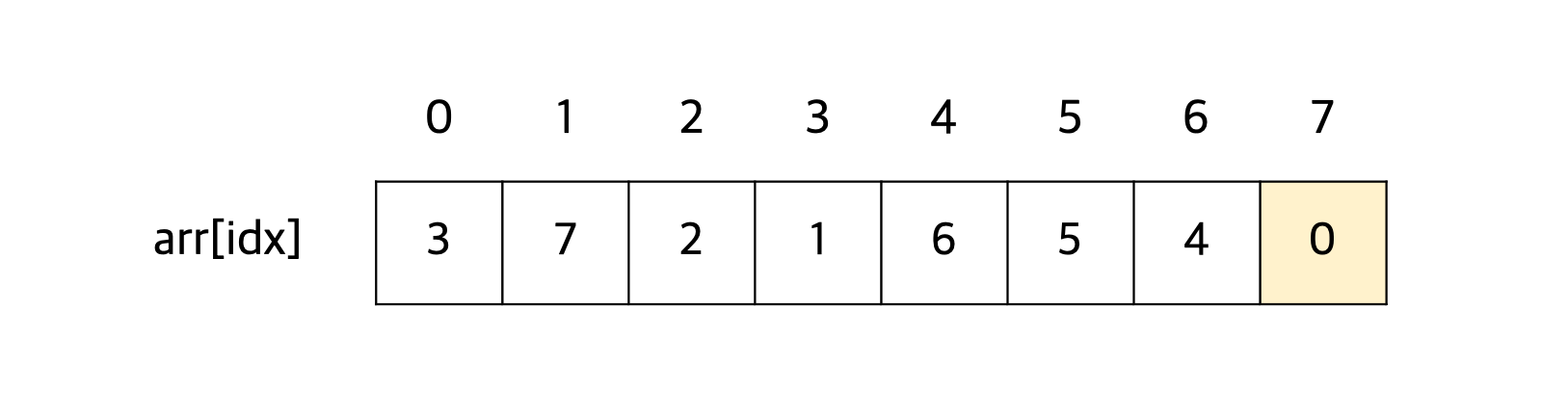
7번째 자리에 위치해야 할 숫자는 인덱스 0번부터 7번까지에 있는 숫자들 중 가장 큰 숫자가 된다.
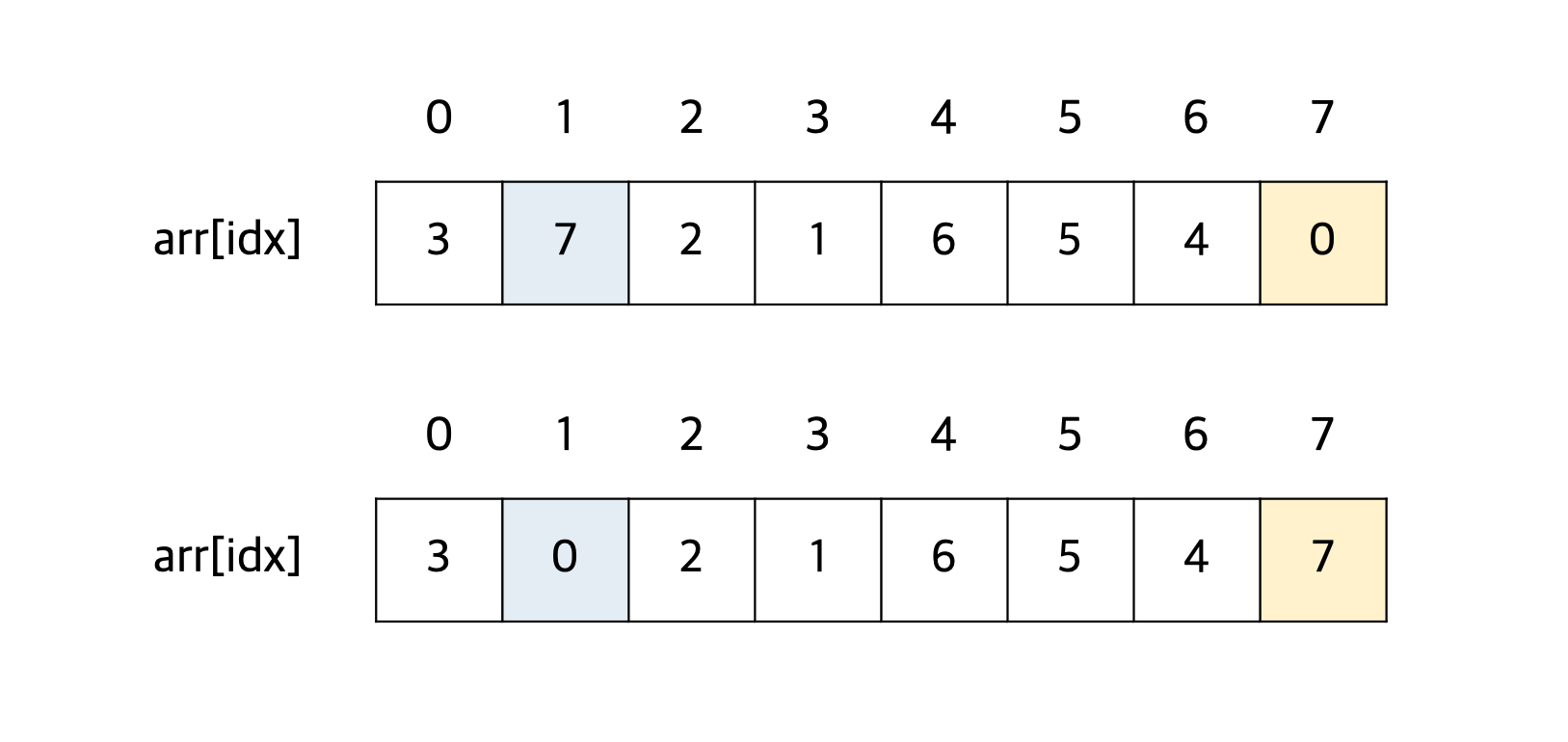
따라서 0번부터 7번까지의 인덱스를 순회하여 가장 큰 숫자가 있는 인덱스 1번을 알아낸다.
이후, 인덱스 7번에 있는 숫자 0과 1번에 있는 숫자 7을 swap() 함수를 이용하여 교환한다.

6번째 자리에 위치해야 할 숫자는 인덱스 0번 부터 6번까지에 있는 숫자들 중 가장 큰 숫자가 된다.

따라서 0번부터 6번까지의 인덱스를 순회하여 남아있는 숫자들 중 가장 큰 숫자가 있는 인덱스 4번을 알아낸다.
이후, 인덱스 6번에 있는 숫자 4와 인덱스 4번에 있는 숫자 6의 자리를 swap() 함수로 교환한다.
이와 같은 과정을 N-1번 반복하여 남아있는 수들 중 가장 큰 수를 각 인덱스로 위치시킨다.
코드
#include <iostream>
using namespace std;
int n = 8;
int arr[8] = {3, 7, 2, 1, 6, 5, 4, 0};
void selectionSort(int st, int en) {
for (int i=n-1; i>0; i--) { //i번째 자리에 위치해야 하는 원소 선택
int maxidx = 0; //남아있는 원소들 중 가장 큰 수가 있는 인덱스
for (int j=1; j<=i; j++) {
if (arr[maxidx] < arr[j]) maxidx = j;
}
swap(arr[i], arr[maxidx]);
}
}
void printarr() {
for (int i=0; i<n; i++)
cout<<arr[i]<<" ";
cout<<endl;
}
int main() {
selectionSort(0, n);
printarr();
return 0;
}
/*output:
0 1 2 3 4 5 6 7 */
선택정렬의 시간 복잡도
외부의 루프를 (N-1)번 도는 동안, 각 자리에 와야하는 최댓값을 구하기 위하여 N-1, N-2, N-3, ... , 1번의 비교연산을 수행한다.
따라서, T(n) = (n-1)+(n-2)+(n-3)+...+1 = (n-1)*n/2
시간복잡도는 O(n) = n^2 이다.
안정성과 제자리성
선택정렬 알고리즘으로 정렬을 수행하는 경우 동일한 값을 가지는 원소들의 본래 순서가 보장되지 않는다. 따라서 선택정렬은 불안정정렬(Unstable sort)이다. 또한, 기존 배열 이외의 추가적인 메모리를 거의 사용하지 않는 제자리 정렬(In-place sort)이다.
'Computer Basics > Algorithm Techniques' 카테고리의 다른 글
| 삽입정렬(Insertion Sort) 개념/시간복잡도/Stable/In-place (0) | 2022.02.11 |
|---|---|
| 버블정렬(Bubble sort) 개념/시간복잡도/Stable/In-place (0) | 2022.02.11 |
| BFS(Breadth First Search) (0) | 2022.01.10 |
| 동적계획법(Dynamic Programming) (0) | 2021.11.17 |
| 소수 판별 알고리즘과 에라토스테네스의 체 (2) | 2021.11.09 |
댓글