동적계획법에 대한 이해
피보나치 수열은 첫째항이 0, 둘째항이 1이고 이전 두항을 더해가며 새로운 항의 값을 구해나가는 수열이다.
0, 1, 1, 2, 3, 5, 8, 13 ... 과 같이 이어지며, 점화식은 다음과 같다.
F(N) = F(N-1) + F(N-2) (N >= 2)
F(0) = 0, F(1) = 1
N번째 항의 값을 구하는 문제는, N-1번째 항을 구하는 문제와 N-2번째 항을 구하는 문제로 나누어질 수 있다. 이렇게 큰 문제를 작은 문제로 나누어 풀 수 있는 경우를 최적 부분 구조(Optimal Structure) 라고 한다. 최적 부분 구조에 대해 자세히 말하면, 문제의 최적 해결 방법이 부분 문제에 대한 최적 해결 방법으로 구성되는 경우를 말한다.
최적 부분 구조를 가지는 피보나치 수열을 재귀 함수로 구현해보자.
int fibonacci(int n) {
if (n <= 1) return n;
return fibonacci(n-1) + fibonacci(n-2);
}
위와 같이 구현하는 경우, 하나의 큰 문제에 대해 작은 문제가 2개씩 파생되어 O(2^N)의 시간 복잡도를 갖는다. 한 가지 중요한 사실은, 작은 부분들의 문제에서 중복이 생긴다.
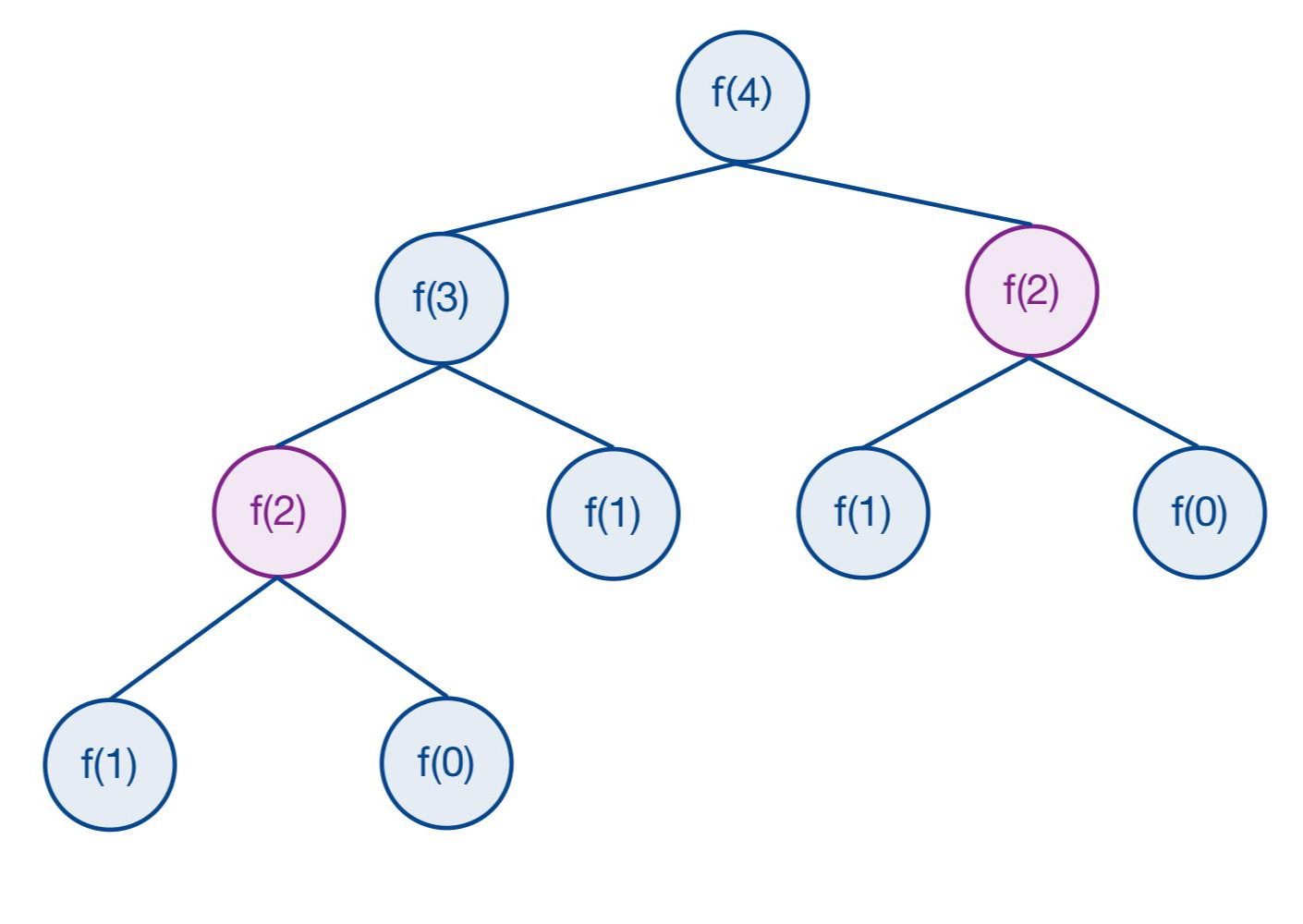
예를 들어, fibonacci(4)를 구한다고 생각해보자. f(2)는 항상 동일한 값을 가짐에도 불구하고 f(2)가 필요할 때마다(등장할 때마다) 새로 구해주어야 한다. 이와 같은 상황을 중복되는 하위 문제들(Overlapping Subproblems) 이라 표현하는데, 동적 계획법은 1) 최적 부분 구조를 갖고 2) 하위 문제들이 중복될 때 유용하게 사용할 수 있다.
동적계획법 의 구현 방법
Top down(Memoization) 방법과 Bottom up(Tabulation) 방법
동적 계획법의 핵심은, 중복되는 하위 문제들의 정답을 저장하여 반복적으로 꺼내 사용하는 것이다. 위의 예시에서 최초로 f(2)를 구했을 때 메모리에 저장해놓고, 다시 f(2)의 값이 필요할 때는 저장된 값을 가져다 씀으로써 반복적인 계산을 피한다. 계산한 값을 저장하면, 동일한 피보나치 문제를 O(N)의 시간 복잡도로 해결할 수 있다.
Top down(Memoization)
DP 문제에 접근할 때, 큰 문제에서 작은 문제로 내려가는 순으로 해결하는 방법을 Top down 방식이라 한다.
피보나치 수열을 Top down 방식으로 구현하면, 다음과 같다. memo 배열에 계산의 결과를 저장하고, 계산 결과가 있으면 그 값을 꺼내어 재사용한다.
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
int memo[10000];
int fibonacci(int n) {
if (n <= 1) return n;
if (memo[n] > 0) return memo[n]; // memo[n]에 이미 값이 들어있는 경우 해당 값 리턴
memo[n] = fibonacci(n-1) + fibonacci(n-2); // fibonacci(n)을 구한적이 없는 경우 계산
return memo[n];
}
int main() {
memset(memo, 0, sizeof(memo));
int re = fibonacci(10);
cout << re;
return 0;
}
Bottom up(Tabulation)
작은 문제들부터 해결하여 큰 문제에 도달하는 것을 Bottom up(Tabulation) 방식이라고 한다. Tabulation의 뜻은 앞에서부터 차례로 표를 채워간다는 의미이다. Tabulation 방식은 재귀가 아닌 반복문을 사용한다.
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
int dp[10000];
int fibonacci(int n) {
dp[0] = 0;
dp[1] = 1;
for (int i=2; i<=n; i++)
dp[i] = dp[i-1] + dp[i-2];
return dp[n];
}
int main() {
int re = fibonacci(10);
cout << re;
return 0;
}'Computer Basics > Algorithm Techniques' 카테고리의 다른 글
| 삽입정렬(Insertion Sort) 개념/시간복잡도/Stable/In-place (0) | 2022.02.11 |
|---|---|
| 버블정렬(Bubble sort) 개념/시간복잡도/Stable/In-place (0) | 2022.02.11 |
| 선택정렬(Selection sort) 개념/시간복잡도/Unstable/In-place (0) | 2022.02.03 |
| BFS(Breadth First Search) (0) | 2022.01.10 |
| 소수 판별 알고리즘과 에라토스테네스의 체 (2) | 2021.11.09 |
댓글