2103번: 직교다각형 복원
첫째 줄에 점의 개수 N(1≤N≤100,000)이 주어진다. 다음 N개의 줄에는 각 점의 x, y(0≤x, y≤10,000)좌표가 주어진다. 이 점들은 직교다각형을 이루는 순서대로 주어지지 않을 수도 있으며, 같은 점이
www.acmicpc.net
직교 다각형이란 모든 변이 x축이나 y축에 평행한 다각형을 말한다. 문제에서 제시한 정사각형 이외에도, 아래와 같은 다양한 직교 다각형을 만들 수 있다.
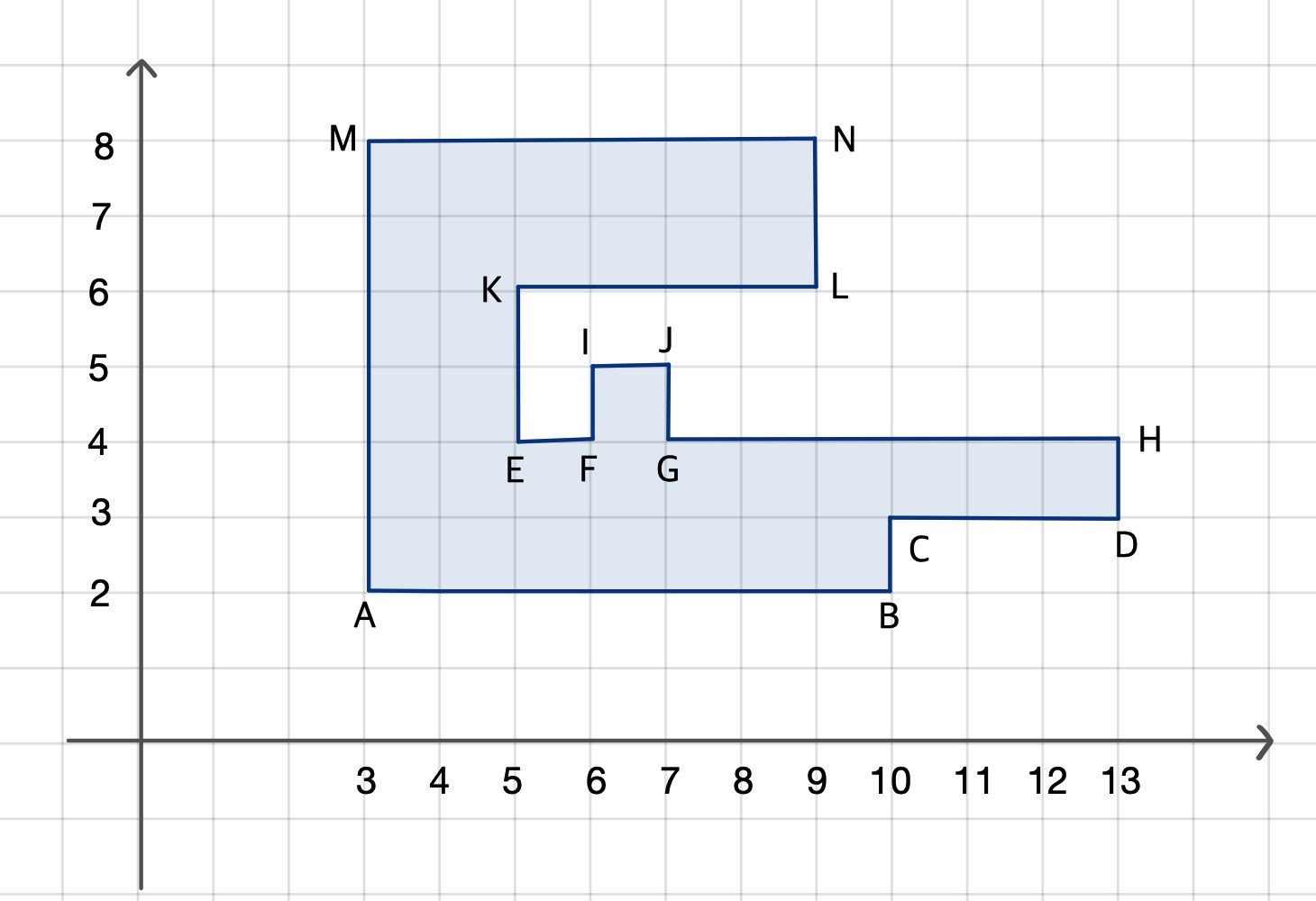
문제에서 요구한 것은 직교 다각형의 꼭짓점들이 주어졌을 때, 둘레를 구하는 것이다. 도형의 둘레는 가로 변들의 합과 세로 변들의 합으로 나누고 이들을 더해 구할 수 있다.
d(A, B)를 A, B 두 점 사이의 거리라 할때,
가로변들의 합
= d(A, B) + d(C, D) + d(E, F) + d(F, G) + d(G, H) + d(I, J) + d(K, L) + d(M, N)
= (y가 2인 두 좌표 A, B를 오름차순으로 정렬한 벡터 {A, B}에서 (A와 B의 차))
+ (y가 3인 두 좌표 C, D를 오름차순으로 정렬한 벡터 {C, D}에서 (C와 D의 차))
+ (y가 4인 네 좌표 E, F, G, H를 오름차순으로 정렬한 벡터 {E, F, G, H}에서 (E와 F의 차) + (G와 H의 차)) ...
따라서 N개의 좌표값을 입력 받을 때, y값을 기준으로 각각의 x값을 저장한다.
//vX[a]: y좌표가 a인 점들의 x좌표 목록
vX[0]
vX[1]
vX[2] 3 10
vX[3] 10 13
vX[4] 5 6 7 13
vX[5] 6 7
vX[6] 5 9
vX[7]
vX[8] 3 9
...
이후, y값들을 순회하면서 v[y]에 저장 된 x 값들을 오름차순으로 정렬하고, v[y]에 저장된 x 좌표를 2개씩 짝지어 차를 구한다. 구한 차는 두점 사이의 거리 이므로 모두 sum에 더해주면 가로 변들의 길이가 모두 더해진다. 세로 변들의 합 역시 가로 변들의 합을 구하는 과정과 동일 하다.
세로변들의 합
= d(A, M) + d(E, K) + d(F, I) + d(G, J) + d(L, N) + d(B, C) + d(D, H)
= (x가 3인 두 좌표 A, M을 오름차순으로 정렬한 벡터 {A, M}에서 (A와 M의 차))
+ (x가 5인 두 좌표 E, K를 오름차순으로 정렬한 벡터 {E, K}에서 (E와 K의 차)) ...
따라서 N개의 좌표를 입력 받을 때 vX를 셋팅함과 동시에 vY 벡터를 구성한다.
//vY[a]: x가 a인 좌표들의 y값 목록
vY[0]
vY[1]
vY[2]
vY[3] 2 8
vY[4]
vY[5] 4 6
vY[6] 4 5
vY[7] 4 5
vY[8]
vY[9] 6 8
...
이후, x값들을 순회하면서 v[x]에 저장된 y값들을 오름차순으로 정렬하고, 2개씩 짝지어 두 값의 차를 구한다. 구한차(두 점사이의 거리)를 sum에 더해주면 세로 변들의 길이가 모두 더해진다.
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <tuple>
using namespace std;
int main() {
int N;
scanf("%d", &N);
vector<vector<int>> vX(10001);
vector<vector<int>> vY(10001);
for (int i=0; i<N; i++) {
int x, y;
scanf("%d %d", &x, &y);
vX[x].push_back(y);
vY[y].push_back(x);
}
int sum = 0;
for (int i=0; i<10001; i++) {
sort(vX[i].begin(), vX[i].end());
sort(vY[i].begin(), vY[i].end());
for (int j=0; j<vX[i].size(); j+=2)
sum += vX[i][j+1]-vX[i][j];
for (int j=0; j<vY[i].size(); j+=2)
sum += vY[i][j+1]-vY[i][j];
}
printf("%d", sum);
return 0;
}'Computer Basics > BOJ Solutions' 카테고리의 다른 글
| [백준 2428번] 표절 풀이 (0) | 2021.09.25 |
|---|---|
| [백준 2121번] 넷이 놀기 풀이 (0) | 2021.09.25 |
| [백준 1448번] 삼각형 만들기 풀이 (0) | 2021.09.25 |
| [백준 16960번] 스위치와 램프 풀이 (0) | 2021.09.25 |
| [백준 11558번] The Game of Death 풀이 (0) | 2021.09.25 |
댓글