문제
11727번: 2×n 타일링 2
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×17 직사각형을 채운 한가지 예이다.
www.acmicpc.net
입력
채워야 하는 직사각형의 가로 길이 N
출력
2*N 직사각형을 1x2, 2x1, 2x2 타일로 채울 수 있는 방법의 수
풀이 방법
DP[N] = 2*N 직사각형을 채울 수 있는 방법의 수로 놓고, 이를 작은 문제들로 나누어 동적 프로그래밍으로 풀이한다.
2*N 직사각형을 만드는(채우는) 방법은 3가지가 있다.
1) 2*(N-1) 직사각형의 오른쪽에 2*1 크기의 타일을 한개 놓는 것

2) 2*(N-2) 직사각형의 오른쪽에 1*2 크기의 타일을 두개 놓는 것
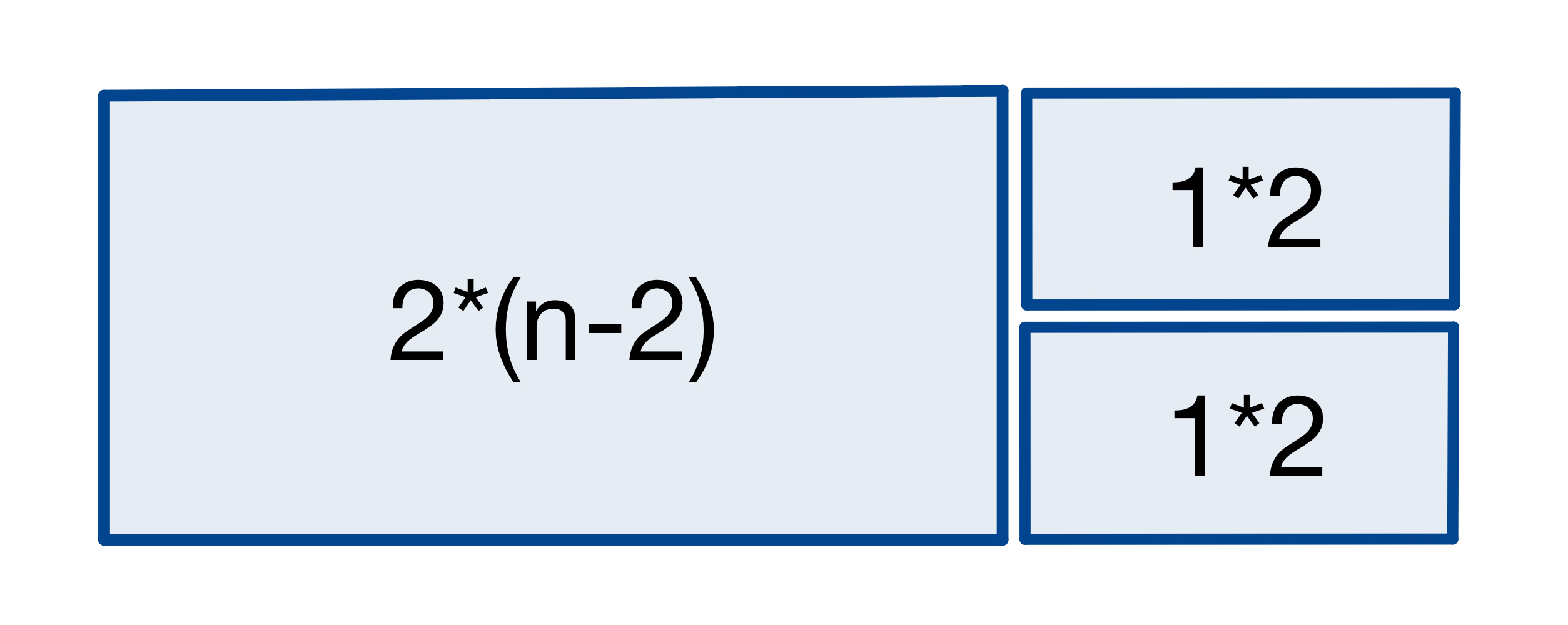
3) 2*(N-2) 직사각형의 오른쪽에 2*2 크기의 타일을 한개 놓는 것

따라서, DP[N] = DP[N-1] + DP[N-2] + DP[N-2] 가 된다.
2*N의 직사각형을 채우는 문제를 더 작은 단위의 문제로 나누어 해결할 수 있는 것이다.
이를 정리하면, DP[N] = DP[N-1] + 2*DP[N-2] 의 점화식이 도출된다.
문제에서는 해당 값을 10007로 나눈 값을 저장하라고 했으므로, 10007씩을 나누며 값을 저장한다.
전체 코드
전체 풀이 코드는 다음과 같다.
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <tuple>
#include <vector>
#include <stack>
#include <queue>
#include <iostream>
using namespace std;
int dp[1001];
int main() {
int N;
scanf("%d", &N);
dp[1] = 1; dp[2] = 3;
for (int i=3; i<=N; i++)
dp[i] = (dp[i-1] + 2*dp[i-2])%10007;
printf("%d", dp[N]);
return 0;
}
'Computer Basics > BOJ Solutions' 카테고리의 다른 글
| [백준 2410번] 2의 멱수의 합 풀이 (0) | 2021.10.20 |
|---|---|
| [백준 2251번] 물통 풀이 (0) | 2021.10.18 |
| [백준 1992번] 쿼드트리 풀이 (0) | 2021.10.15 |
| [백준 1790번] 수 이어 쓰기 2 풀이 (0) | 2021.10.13 |
| [백준 1629번] 곱셈 풀이 (0) | 2021.10.12 |
댓글