16488번: 피카츄가 낸 어려운 문제
맨날 학교 칠판에 이등변삼각형을 그리고 노는 피카츄가 어느 날, 칠판에 변 AB와 변 AC의 길이가 모두 N인 이등변 삼각형을 그린 다음, 친구들에게 아래와 같은 문제를 냈다. 이등변삼각형 ABC에
www.acmicpc.net
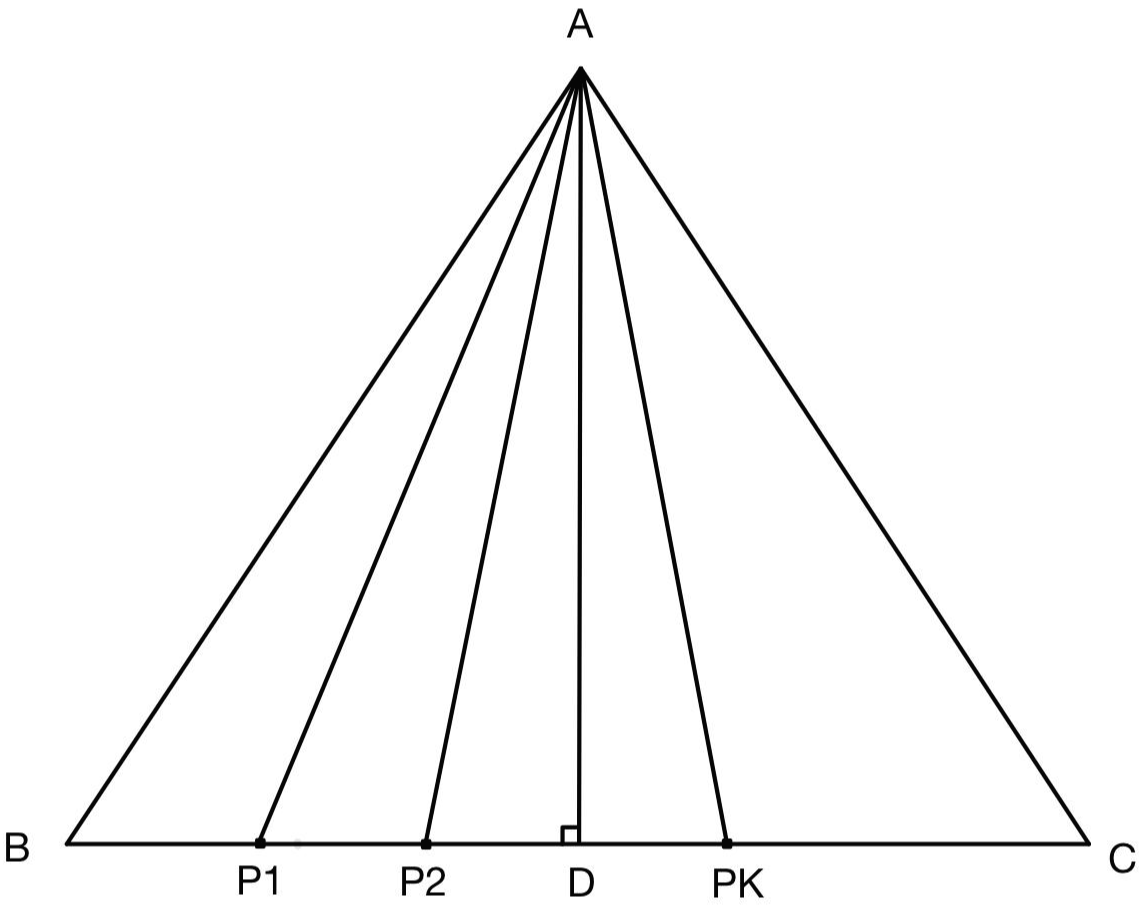
변 AB = AC인 이등변 삼각형의 밑변 BC에 P1 ... PK 까지의 점을 두었다.
우리가 구해야 하는 값은 다음과 같다.
$$ \sum_{i=1}^K F(i) = \sum_{i=1}^K ( \overline{APi}^2 + \overline{BPi} * \overline{CPi} ) $$
먼저, APi^2 을 계산해보자. 삼각형 A Pi D 는 직각삼각형을 이루고 있으므로 피타고라스 공식에 의해 다음과 같다.
$$ \overline{APi}^2 = (\overline{BD} - \overline{BPi})^2 + \overline{AD}^2 $$
$$ \overline{APi}^2 = (\frac{1}{2} * \overline{BC} - \overline{BPi})^2 + \overline{AD}^2 $$
BPi * CPi 를 계산해보자.
$$\overline{BPi} * \overline{CPi} = \overline{BPi} * ( \overline {BC} - \overline{BPi} )$$
따라서 F(i) = APi^2 + BPi * CPi 는 다음과 같이 계산된다.
$$ F(i) = \overline{APi}^2 + \overline{BPi} * \overline{CPi}$$
$$= (\frac{1}{2} * \overline{BC} - \overline{BPi})^2 + \overline{AD}^2 + \overline{BPi} * ( \overline {BC} - \overline{BPi} ) $$
$$ = (\frac{1}{2} \overline{BC})^2 + \overline {AD}^2 $$
이등변 삼각형의 두 변의 길이 N이 주어지고, 삼각형 ABD는 직각 삼각형 이므로,
$$ (\frac{1}{2} \overline{BC})^2 + \overline {AD}^2 = N^2 $$
최종적으로 F(i)는 다음과 같다.
$$F(i) = N^2$$
따라서 우리가 구하고자 하는 값은,
$$ \sum_{i=1}^K F(i) = \sum_{i=1}^K ( \overline{APi}^2 + \overline{BPi} * \overline{CPi} ) $$
$$ = \sum_{i=1}^K N^2 = K * N^2 $$
값을 출력할 때 K와 N의 곱셈 결과가 오버플로우 되지 않도록 자료형만 신경써주면 된다.
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <tuple>
using namespace std;
int main() {
long long N, K;
scanf("%lld %lld", &N, &K);
printf("%lld", N*N*K);
return 0;
}
'Computer Basics > BOJ Solutions' 카테고리의 다른 글
| [백준 14465번] 소가 길을 건너간 이유 5 풀이 (0) | 2021.10.05 |
|---|---|
| [백준 10819번] 차이를 최대로 풀이 (0) | 2021.10.04 |
| [백준 14930번] 구슬 (BEAD) 풀이 (0) | 2021.10.02 |
| [백준 538번] 제곱근 작도 풀이 (0) | 2021.09.30 |
| [백준 2504번] 괄호의 값 풀이 (0) | 2021.09.30 |
댓글