해설
2x1(1x2) 모양의 직사각형으로 3xn 직사각형을 채우는 경우의 수를 구하는 문제이다.
n을 하나씩 늘려가면서 규칙을 찾아보자.
1. n = 1 일 때
주어진 직사각형으로 3 x 1 직사각형을 채울 수 없다.
n = 1 뿐만 아니라 n이 홀수이면 무조건 채울 수 없다는 사실을 알 수 있다.
2. n = 2 일 때
3가지 방법으로 채울 수 있다.

즉, d[2] = 3
3. n = 4 일 때
(1) 앞의 두 칸을 먼저 채우고 나머지를 3x2 직사각형을 채우는 방법으로 채운다. (3 x dp[2])
(2) 네 칸을 전역에 걸쳐 채운다. (2)
(네 칸을 전역에 걸쳐 채우는 방법은 다음과 같다.)

즉, dp[4] = 3 x dp[2] + 2
4. n = 6 일 때
(1) 앞의 두 칸을 먼저 채우고 나머지를 3 x 4 직사각형을 채우는 방법으로 채운다. (3 x dp[4])
(2) 앞의 네 칸을 먼저 전역에 걸쳐 채우고 나머지를 3 x 2 직사각형을 채우는 방법으로 채운다. (2 x dp[2])
(3) 여섯 칸을 전역에 걸쳐 채운다. (2)
(여섯 칸을 전역에 걸쳐 채우는 방법은 다음과 같다.)
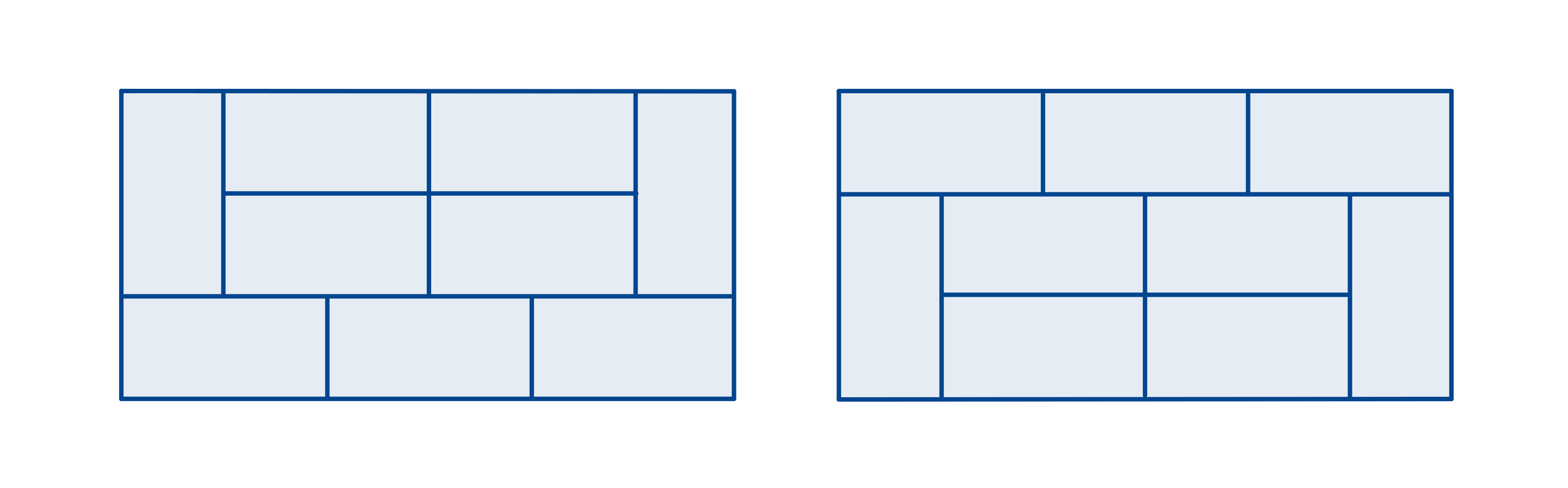
즉, dp[6] = 3 x dp[4] + 2 x dp[2] + 2
5. n = 8 일 때
(1) 앞의 두 칸을 먼저 채우고 나머지를 3 x 6 직사각형을 채우는 방법으로 채운다. (3 x dp[6])
(2) 앞의 네 칸을 먼저 전역에 걸쳐 채우고 나머지를 3 x 4 직사각형을 채우는 방법으로 채운다. (2 x dp[4])
(3) 앞의 여섯 칸을 먼저 전역에 걸쳐 채우고 나머지를 3 x 2 직사각형을 채우는 방법으로 채운다. (2 x dp[2])
(4) 여덟 칸을 전역에 걸쳐 채운다. (2)
(여덟 칸을 전역에 걸쳐 채우는 방법은 다음과 같다.)

즉, dp[8] = 3 x dp[6] + 2 x dp[4] + 2 x dp[2] + 2
...
규칙을 잘 살펴보면, 점화식은 다음과 같다.
dp[n] = 3 x dp[n-2] + 2 x dp[n-4] + 2 x dp[n-2] + ... + 2 x dp[0] (n은 짝수, dp[0] = 1)
dp[n] = 0 (n은 홀수)
dp[n]을 구해 리턴하면 정답이다.
코드
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <tuple>
#include <vector>
#include <stack>
#include <queue>
#include <deque>
#include <set>
#include <map>
#include <unordered_set>
#include <unordered_map>
#include <iostream>
using namespace std;
using ii = pair<int, int>;
using iii = tuple<int, int, int>;
#define X first
#define Y second
#define MOD 1000000007
int solution(int n) {
vector<long long> dp(5005, 0);
dp[0] = 1; dp[2] = 3;
for (int i=4; i<=n; i+=2) {
dp[i] = 3*dp[i-2];
for (int j=i-4; j>=0; j-=2)
dp[i] += 2*dp[j];
dp[i] %= MOD;
}
return dp[n];
}
'Computer Basics > Programmers Solutions' 카테고리의 다른 글
| [프로그래머스 lv3] 순위 풀이 (0) | 2022.08.27 |
|---|---|
| [프로그래머스 lv3] 가장 먼 노드 풀이 (0) | 2022.08.27 |
| [프로그래머스 lv2] 스킬 트리 풀이 (0) | 2022.08.25 |
| [프로그래머스 lv2] 배달 풀이 (0) | 2022.08.25 |
| [프로그래머스 lv2] 쿼드 압축 후 개수 세기 풀이 (0) | 2022.08.25 |
댓글