해설
문제를 처음 딱 보고, 아 뭔가 규칙을 찾는 문제구나 하는 생각이 든다.
h*w의 직사각형에서 대각선이 지나가는 칸 수를 알 수 있다면 전체 블럭의 개수에서 해당 칸의 개수를 빼 정답을 구할 수 있다.
그렇다면 대각선이 지나가는 칸 수는 어떻게 알 수 있을까?
예제로 나온 8*12의 직사각형을 보면, 일정한 패턴이 반복되는 것을 알 수 있다.
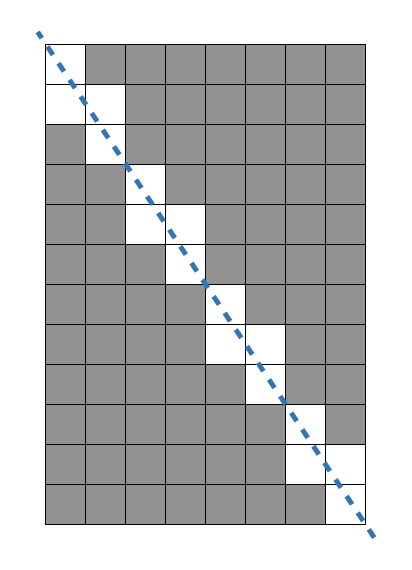
8과 12의 최대공약수 4로 가로와 세로를 각각 나누어보면 2*3의 직사각형이 나온다.
이 직사각형은 전체 직사각형 안에 최대공약수(4개) 만큼 반복된다.

이 작은 직사각형을 보면, 대각선이 지나는 칸의 개수는 2+3-1 = 4개가 된다.
즉, W*H 의 전체 직사각형이 있고, W와 H의 최대공약수를 g라 할 때, W/g * H/g 직사각형 내 대각선이 지나가는 칸의 개수는 W/g+H/g-1 이다. 작은 직사각형은 전체 직사각형 내 g번 반복되므로, 전체 직사각형에서 대각선이 지나가는 칸의 총 개수는 (W/g + H/g -1) * g 가 된다.
따라서 전체 직사각형에서 대각선이 지나가지 않는 칸의 개수는 W*H-(W/g + H/g - 1) * g 이다.
주의 할 것
문제에서 제시된 solution 함수에서 입력값 w와 h는 int 형이다. 하지만 최대 값은 1억이므로 두 w와 h가 모두 1억일 때 두 수의 곱은 int 범위를 넘어가게 된다. 따라서 정답을 리턴할 때 h*w 값이 오버플로우가 발생하지 않도록 1LL를 앞에 곱해준다.
코드
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <tuple>
#include <vector>
#include <stack>
#include <deque>
#include <set>
#include <map>
#include <iostream>
using namespace std;
using ii = pair<int, int>;
using iii = tuple<int, int, int>;
#define X first
#define Y second
long long gcd(long long a, long long b) {
if (b == 0) return a;
return gcd(b, a%b);
}
long long solution(int w,int h) {
long long g = gcd(h, w);
return 1LL*h*w-(h/g+w/g-1)*g;
}
'Computer Basics > Programmers Solutions' 카테고리의 다른 글
| [프로그래머스 lv2] 기능개발 풀이 (0) | 2022.08.09 |
|---|---|
| [프로그래머스 lv2] 124나라의 숫자 풀이 (0) | 2022.08.09 |
| [프로그래머스 lv2] 양궁대회 풀이 (0) | 2022.03.24 |
| [프로그래머스 lv2] 주차요금계산 풀이 (0) | 2022.03.24 |
| [프로그래머스 lv2] k진수에서 소수 개수 구하기 풀이 (0) | 2022.03.22 |
댓글